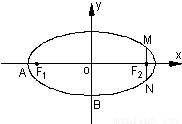
题目内容
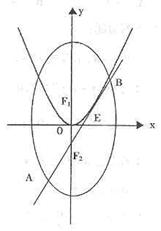
如图,椭圆C: 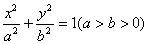 的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线
的焦点为F1(0,c)、F2(0,一c)(c>0),抛物线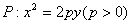 的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且
的焦点与F1重合,过F2的直线l与抛物线P相切,切点在第一象限,且与椭圆C相交于A、B两点,且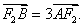
(I)求证:切线l的斜率为定值;
|
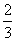 ,求抛物线P的方程;
,求抛物线P的方程;
(III)当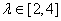 时,求椭圆离心率e的取值范围。
时,求椭圆离心率e的取值范围。
【答案】
解:(I)依题意抛物线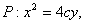
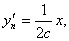 设直线l与抛物线P的切点为
设直线l与抛物线P的切点为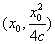 ,又切点在第一象限,
,又切点在第一象限,
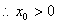
则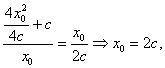
所以切线l的斜率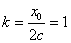 为定值。 ………………4分
为定值。 ………………4分
(文)解:设直线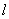 的斜率
的斜率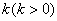 ,则直线l的方程为:
,则直线l的方程为: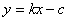
由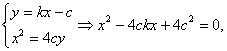
令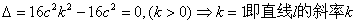 为定值。
为定值。
(II)由(I)可得:
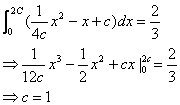
以抛物线P的方程为: ………………8分
………………8分
(III)由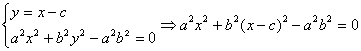 ,
,
由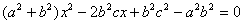
设
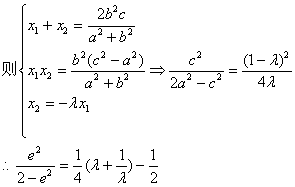
又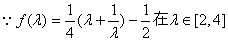 上单调递增,
上单调递增,

(文)解:(I)同理(I)
(II)抛物线P与直线l切于点E,由(1)可得 ,
,
又△OEF2面积为1,
所以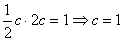
所以抛物线P的方程为: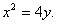 ………………8分
………………8分
又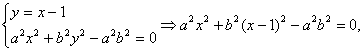
即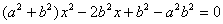 ………………10分
………………10分
设
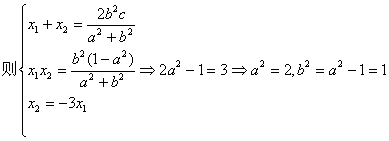
所以所求椭圆方程为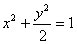 ………………13分
………………13分

练习册系列答案
相关题目
 如图,在直角坐标系xOy中,已知椭圆C:
如图,在直角坐标系xOy中,已知椭圆C:

 +
+ =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e= ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的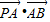 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.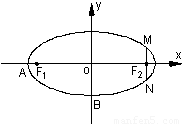
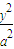 +
+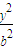 =1(a>b>0)的离心率e=
=1(a>b>0)的离心率e=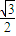 ,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的
,左右两个焦分别为F1、F2.过右焦点F2且与轴垂直的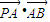 =m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.
=m-4,(m∈R)试求点P的轨迹方程,使点B关于该轨迹的对称点落在椭圆C上.