题目内容
【题目】已知 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() ,
, ![]() ,点
,点 ![]() 在椭圆上,
在椭圆上, ![]() ,且
,且 ![]() 的面积为4.
的面积为4.
(1)求椭圆的方程;
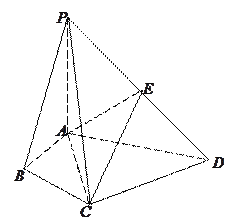
(2)点 ![]() 是椭圆上任意一点,
是椭圆上任意一点, ![]() 分别是椭圆的左、右顶点,直线
分别是椭圆的左、右顶点,直线 ![]() 与直线
与直线 ![]() 分别交于
分别交于 ![]() 两点,试证:以
两点,试证:以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于定点,并求该定点的坐标.
轴于定点,并求该定点的坐标.
【答案】
(1)解;因为 ![]() ,所以
,所以 ![]() ,
, ![]() .
.
由题意得 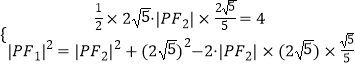 ,解得
,解得 ![]() .
.
从而 ![]() ,结合
,结合 ![]() ,得
,得 ![]() ,
,
故椭圆的方程为 ![]() .
.
(2)解:由(1)得 ![]() ,
, ![]() ,
,
设 ![]() ,则直线
,则直线 ![]() 的方程为
的方程为 ![]() ,
,
它与直线 ![]() 的交点的坐标为
的交点的坐标为 ![]() ,
,
直线 ![]() 的方程为
的方程为 ![]() ,它与直线
,它与直线 ![]() 的交点的坐标为
的交点的坐标为 ![]() ,
,
再设以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于点
轴于点 ![]() ,则
,则 ![]() ,从而
,从而 ![]() ,即
,即 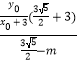
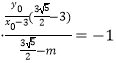 ,即
,即 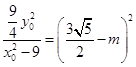 ,解得
,解得 ![]() .
.
故以 ![]() 为直径的圆交
为直径的圆交 ![]() 轴于定点,该定点的坐标为
轴于定点,该定点的坐标为 ![]() 或
或 ![]() .
.
【解析】(1) 由已知求出![]() PF2F1的正弦和余弦值,再利用面积公式
PF2F1的正弦和余弦值,再利用面积公式![]() 以及余弦定理
以及余弦定理![]() 可求得点P到两焦点的距离,求出a的值进而得到b的值故可求出椭圆的方程。(2)由(1)的方程求出两个定点的坐标,设出点M的坐标得到直线的方程,进而可求出点E、F的坐标,利用两条直线垂直斜率之积等于-1即可求出m的值。
可求得点P到两焦点的距离,求出a的值进而得到b的值故可求出椭圆的方程。(2)由(1)的方程求出两个定点的坐标,设出点M的坐标得到直线的方程,进而可求出点E、F的坐标,利用两条直线垂直斜率之积等于-1即可求出m的值。

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目