题目内容
已知平面上两定点A、B的距离是2，动点M满足条件
=1，则动点M的轨迹是
- A.直线
- B.圆
- C.椭圆
- D.双曲线
B
分析：建立直角坐标系，利用向量的数量积公式得到动点的轨迹方程，据圆的方程的特点得到轨迹．
解答：以AB所在直线为x轴，以AB的中垂线为y轴建立直角坐标系，则
A（-1，0） B（1，0）
设M（x，y）则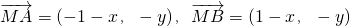
∴（-1-x）（1-x）+y2=1
x2+y2=2
故选B
点评：本题考查向量的数量积公式对应坐标乘积的和、圆方程的形式：（x-a）2+（y-b）2=r2
分析：建立直角坐标系，利用向量的数量积公式得到动点的轨迹方程，据圆的方程的特点得到轨迹．
解答：以AB所在直线为x轴，以AB的中垂线为y轴建立直角坐标系，则
A（-1，0） B（1，0）
设M（x，y）则
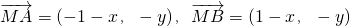
∴（-1-x）（1-x）+y2=1
x2+y2=2
故选B
点评：本题考查向量的数量积公式对应坐标乘积的和、圆方程的形式：（x-a）2+（y-b）2=r2
练习册系列答案
相关题目
下列说法正确的是（ ）
| A、△ABC中，已知A（1，1），B（4，1），C（2，3），则AB边上的高的方程是x=2 | ||
| B、方程y=x2（x≥0）的曲线是抛物线 | ||
C、已知平面上两定点A、B，动点P满足|PA|-|PB|=
| ||
| D、第一、三象限角平分线的方程是y=x |
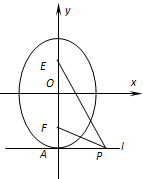（1）已知平面上两定点A（-2，0）．B（2，0），且动点M标满足
（2007•金山区一模）（1）已知平面上两定点A（-2，0）、B（2，0），且动点M的坐标满足
=0，求动点M的轨迹方程；
长轴顶点A且与长轴垂直的直线，E、F是两个焦点，点P∈l，P不与A重合．若∠EPF=α，证明：
．类比此结论到双曲线
，l是经过焦点F且与实轴垂直的直线，A、B是两个顶点，点P∈l，P不与F重合（如图2）．若∠APB=α，试求角α的取值范围．