题目内容
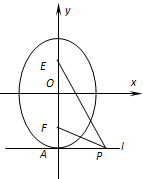 (1)已知平面上两定点A(-2,0).B(2,0),且动点M标满足
(1)已知平面上两定点A(-2,0).B(2,0),且动点M标满足| MA |
| MB |
(2)若把(1)的M的轨迹图象向右平移一个单位,再向下平移一个单位,恰与直线x+ky-3=0 相切,试求实数k的值;
(3)如图,l是经过椭圆
| y2 |
| 25 |
| x2 |
| 16 |
并将此题类比到双曲线:
| y2 |
| 25 |
| x2 |
| 16 |
分析:(1)设点M为(x,y)代入题目中的条件
•
=0可得x2+y2=4即得到点M的轨迹方程.
(2)由题意得得到新的圆的方程(x-1)2+(y+1)2=4,由其与直线x+ky-3=0 相切可得k=0或k=
.
(3)(ⅰ)由题得α=∠EPA-∠FPA,所以tanα=tan(∠EPA-∠FPA),可得0<tanα≤
即0<α≤arctan
(ⅱ)类比椭圆的证明方法得到双曲线的类似的性质0<α≤arctan
.
| MA |
| MB |
(2)由题意得得到新的圆的方程(x-1)2+(y+1)2=4,由其与直线x+ky-3=0 相切可得k=0或k=
| 4 |
| 3 |
(3)(ⅰ)由题得α=∠EPA-∠FPA,所以tanα=tan(∠EPA-∠FPA),可得0<tanα≤
| 3 |
| 4 |
| 3 |
| 4 |
(ⅱ)类比椭圆的证明方法得到双曲线的类似的性质0<α≤arctan
| 5 |
| 4 |
解答: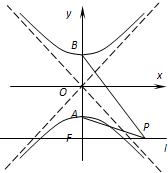 解:(1)设M(x,y),由
解:(1)设M(x,y),由
•
=0得x2+y2=4,此即点M的轨迹方程.
(2)将x2+y2=4向右平移一个单位,再向下平移一个单位后,
得到圆(x-1)2+(y+1)2=4
依题意有
=2,得k=0或k=
.
(3)(ⅰ)证明:不妨设点P在A的右侧,并设P(t,-5)(t>0),
则tan∠EPA=
,tan∠FPA=
所以tanα=tan(∠EPA-∠FPA)=
=
≤
所以0<tanα≤
.显然α为锐角,即:0<α≤arctan
(ⅱ)如图.(图形中没有体现出双曲线的渐近性的,扣1分)0<α≤arctan
.
 解:(1)设M(x,y),由
解:(1)设M(x,y),由| MA |
| MB |
(2)将x2+y2=4向右平移一个单位,再向下平移一个单位后,
得到圆(x-1)2+(y+1)2=4
依题意有
| |k+2| | ||
|
| 4 |
| 3 |
(3)(ⅰ)证明:不妨设点P在A的右侧,并设P(t,-5)(t>0),
则tan∠EPA=
| 8 |
| t |
| 2 |
| t |
所以tanα=tan(∠EPA-∠FPA)=
| ||||
1+
|
| 6 | ||
t+
|
| 3 |
| 4 |
所以0<tanα≤
| 3 |
| 4 |
| 3 |
| 4 |
(ⅱ)如图.(图形中没有体现出双曲线的渐近性的,扣1分)0<α≤arctan
| 5 |
| 4 |
点评:解决此类问题的关键是把向量条件坐标化,熟练掌握直线与圆的位置关系以及椭圆与双曲线的几何性质.

练习册系列答案
相关题目
 、
、 ,P为一个动点,且满足
,P为一个动点,且满足
 .
. .分别以A、B为切点作轨迹C的切线,设其交点为Q,证明
.分别以A、B为切点作轨迹C的切线,设其交点为Q,证明 为定值.
为定值.