题目内容
已知A(1,f'(1))是函数y=f(x)的导函数图象上的一点,点B为(x,ln(x+1)),向量 ,令
,令 .
.(1)求函数y=f(x)的表达式;
(2)若x>0,证明:
 ;
;(3)若x∈[-1,1]时,不等式
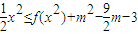 都恒成立,求实数m的取值范围.
都恒成立,求实数m的取值范围.
【答案】分析:(1)先求出 ,再由向量数量积的坐标运算法则得f(x)的解析式,求导后可得f'(1),从而可得函数y=f(x)的表达式
,再由向量数量积的坐标运算法则得f(x)的解析式,求导后可得f'(1),从而可得函数y=f(x)的表达式
(2)构造新函数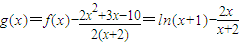 ,利用导数只需证明函数g(x)在(0,+∞)的下界大于零即可
,利用导数只需证明函数g(x)在(0,+∞)的下界大于零即可
(3)参变分离可得 x∈[-1,1]时恒成立,下面只需求函数
x∈[-1,1]时恒成立,下面只需求函数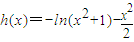 的最大值即可,利用导数可求这个值,再解不等式即可求实数m的取值范围
的最大值即可,利用导数可求这个值,再解不等式即可求实数m的取值范围
解答:解:(1)∵A(1,f'(1)),B(x,ln(x+1)),∴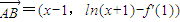
∴f(x)=ln(x+1)+x-f'(1)-1,∴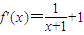 ,∴
,∴ ∴
∴
(2)设 ∴
∴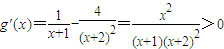
在(0,+∞)上是增函数,又∵g(0)=0∴g(x)>0,∴
(3)由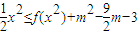 得
得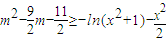
设 ,∴
,∴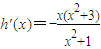 ∴当x∈[-1,0]时,h'(x)>0,h(x)为递增;
∴当x∈[-1,0]时,h'(x)>0,h(x)为递增;
当x∈[0,1]时,h'(x)<0,h(x)为递减
∴h(x)max=h(0)=0,∴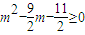 ,解得m≤-1或
,解得m≤-1或
∴实数m的取值范围是m≤-1或
点评:本题考查了导数的计算,导数证明不等式,导数求最值的方法,解题时要耐心细致,善于构造新函数解决函数关系问题,对恒成立问题,要多加总结
 ,再由向量数量积的坐标运算法则得f(x)的解析式,求导后可得f'(1),从而可得函数y=f(x)的表达式
,再由向量数量积的坐标运算法则得f(x)的解析式,求导后可得f'(1),从而可得函数y=f(x)的表达式(2)构造新函数
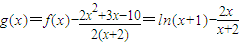 ,利用导数只需证明函数g(x)在(0,+∞)的下界大于零即可
,利用导数只需证明函数g(x)在(0,+∞)的下界大于零即可(3)参变分离可得
 x∈[-1,1]时恒成立,下面只需求函数
x∈[-1,1]时恒成立,下面只需求函数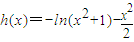 的最大值即可,利用导数可求这个值,再解不等式即可求实数m的取值范围
的最大值即可,利用导数可求这个值,再解不等式即可求实数m的取值范围解答:解:(1)∵A(1,f'(1)),B(x,ln(x+1)),∴
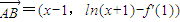
∴f(x)=ln(x+1)+x-f'(1)-1,∴
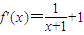 ,∴
,∴ ∴
∴
(2)设
 ∴
∴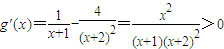
在(0,+∞)上是增函数,又∵g(0)=0∴g(x)>0,∴

(3)由
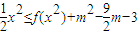 得
得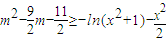
设
 ,∴
,∴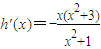 ∴当x∈[-1,0]时,h'(x)>0,h(x)为递增;
∴当x∈[-1,0]时,h'(x)>0,h(x)为递增;当x∈[0,1]时,h'(x)<0,h(x)为递减
∴h(x)max=h(0)=0,∴
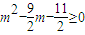 ,解得m≤-1或
,解得m≤-1或
∴实数m的取值范围是m≤-1或

点评:本题考查了导数的计算,导数证明不等式,导数求最值的方法,解题时要耐心细致,善于构造新函数解决函数关系问题,对恒成立问题,要多加总结

练习册系列答案
相关题目