题目内容
已知函数f(x)是可导函数,且满足
=-1,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是( )
| lim |
| x→0 |
| f(1)-f(1-x) |
| x |
分析:函数f(x)是可导函数,且满足
=-1,可得
=-1,利用导数的定义,即可求得切线斜率.
| lim |
| x→0 |
| f(1)-f(1-x) |
| x |
| lim |
| x→0 |
| f(1)-f(1-x) |
| 1-(1-x) |
解答:解:∵函数f(x)是可导函数,且满足
=-1,
∴
=-1
∴f′(1)=-1
∴在曲线y=f(x)上的点A(1,f(1))的切线斜率是-1
故选A.
| lim |
| x→0 |
| f(1)-f(1-x) |
| x |
∴
| lim |
| x→0 |
| f(1)-f(1-x) |
| 1-(1-x) |
∴f′(1)=-1
∴在曲线y=f(x)上的点A(1,f(1))的切线斜率是-1
故选A.
点评:本题考查导数的概念与导数的几何意义,解题的关键是正确理解导数的概念.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
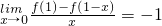 ,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是
,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是 ,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是( )
,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是( )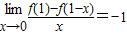 ,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是( )
,则在曲线y=f(x)上的点A(1,f(1))的切线斜率是( )