题目内容

【题目】已知等比数列{an}的各项均为正数，且a1a100+a3a98=8，则log2a1+log2a2+…+log2a100=（ ）
A.10
B.50
C.100
D.1000

【答案】C
【解析】解：∵数列{an}为各项均为正数的等比数列，且a1a100+a3a98=8，
∴a1a100=a2a99=a3a98=…=a50a51=4，
∴log2a1a100=log24=2，
即log2a1+log2a100=log2a2+log2a99=…=log2a50+log2a51=2，
∴log2a1+log2a2+…+log2a100
=（log2a1+log2a100）+（log2a2+log2a99）+…+（log2a50+log2a51）=2×50=100．
故选：C．
【考点精析】掌握数列的前n项和是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系．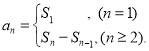

练习册系列答案
相关题目

【题目】由于渤海海域水污染严重，为了获得第一手的水文资料，潜水员需要潜入水深为60米的水底进行作业，根据经验，潜水员下潜的平均速度为（米/单位时间），每单位时间消耗氧气（升），在水底作业10个单位时间，每单位时间消耗氧气（升），返回水面的平均速度为（米/单位时间），每单位时间消耗氧气（升），记该潜水员完成此次任务的消耗氧气总量为（升）.

（1）求关于的函数关系式；

（2）若，求当下潜速度取什么值时，消耗氧气的总量最少.

【题目】交通指数是交通拥堵指数的简称，是综合反映道路网畅通或拥堵的概念，记交通指数为，其范围为，分为五个级别， 畅通； 基本畅通； 轻度拥堵； 中度拥堵； 严重拥堵.早高峰时段（），从某市交通指挥中心随机选取了三环以内的50个交通路段，依据其交通指数数据绘制的频率分布直方图如图.

（1）这50个路段为中度拥堵的有多少个？

（2）据此估计，早高峰三环以内的三个路段至少有一个是严重拥堵的概率是多少？

（3）某人上班路上所用时间若畅通时为20分钟，基本畅通为30分钟，轻度拥堵为36分钟，中度拥堵为42分钟，严重拥堵为60分钟，求此人所用时间的数学期望.

【题目】已知动圆过定点且与圆相切，记动圆圆心的轨迹为曲线.

（1）求曲线的方程；

（2）过点且斜率不为零的直线交曲线于， 两点，在轴上是否存在定点，使得直线的斜率之积为非零常数？若存在，求出定点的坐标；若不存在，请说明理由.

【题目】已知数列{an}中的前n项和为Sn= ，又an=log2bn ．
（1）求数列{an}的通项公式；
（2）求数列{bn}的前n项和Tn ．

【题目】某市为了鼓励市民节约用水，实行“阶梯式”水价，将该市每户居民的月用水量划分为三档：月用水量不超过4吨的部分按2元/吨收费，超过4吨但不超过8吨的部分按4元/吨收费，超过8吨的部分按8元/吨收费.

（1）求居民月用水量费用（单位：元）关于月用电量（单位：吨）的函数解析式；

（2）为了了解居民的用水情况，通过抽样，获得今年3月份100户居民每户的用水量，统计分析后得到如图所示的频率分布直方图，若这100户居民中，今年3月份用水费用不超过16元的占60%，求的值；

（3）若地区居民用水量平均值超过6吨，则说明该地区居民用水没有节约意识在满足（2）的条件下，请你估计市居民用水是否有节约意识（同一组中的数据用该组区间的中点值作代表）.

【题目】（文科）某出租车公司响应国家节能减排的号召，已陆续购买了140辆纯电动汽车作为运营车辆，目前我国主流纯电动汽车按续驶里程数（单位：公里）分为3类，即， ， .对这140辆车的行驶总里程进行统计，结果如下表：

（1）从这140辆汽车中任取1辆，求该车行驶总里程超过5万公里的概率； （2）公司为了了解这些车的工作状况，决定抽取14辆车进行车况分析，按表中描述的六种情况进行分层抽样，设从类车中抽取了辆车. （ⅰ）求的值； （ⅱ）如果从这辆车中随机选取2辆车，求恰有1辆车行驶总里程超过5万公里的概率.

【题目】已知函数f（x）= ．
（1）求证：f（x）+f（1﹣x）= ；
（2）设数列{an}满足an=f（0）+f（ ）+f（ ）+…+f（ ）+f（1），求an；
（3）设数列{an}的前项n和为Sn ， 若Sn≥λan（n∈N*）恒成立，求实数λ的取值范围．

【题目】某企业为了解下属某部门对本企业职工的服务情况，随机访问50名职工，根据这50名职工对该部门的评分，绘制频率分布直方图（如图所示），其中样本数据分组区间为[40，50]，[50，60]，…，[80，90]，[90，100]

（1）求频率分布图中a的值；
（2）估计该企业的职工对该部门评分不低于80的概率；
（3）从评分在[40，60]的受访职工中，随机抽取2人，求此2人评分都在[40，50]的概率．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网