题目内容
(2012•金华模拟)设实数x,y满足不等式组
,则x2+y2的最小值为
.
|
| 1 |
| 2 |
| 1 |
| 2 |
分析:先根据条件画出可行域,z=x2+y2,再利用几何意义求最值,只需求出什么时候可行域内的点到原点距离的最小值,即可求出结论.
解答: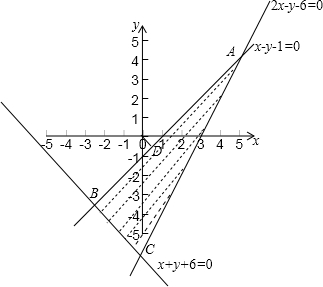 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,
z=x2+y2,
表示可行域内点(x,y)到原点距离的平方,
由图可得,当过原点向直线x-y-1=0作垂线时,垂足到原点的距离最小,
此时垂足到原点的距离为
=
.
即z最小为(
)2=
.
故x2+y2的最小值为:
.
故答案为:
.
 解:先根据约束条件画出可行域,
解:先根据约束条件画出可行域,z=x2+y2,
表示可行域内点(x,y)到原点距离的平方,
由图可得,当过原点向直线x-y-1=0作垂线时,垂足到原点的距离最小,
此时垂足到原点的距离为
| |0-0-1| | ||
|
| ||
| 2 |
即z最小为(
| ||
| 2 |
| 1 |
| 2 |
故x2+y2的最小值为:
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查了简单的线性规划,以及利用几何意义求最值,属于基础题.解决时,首先要解决的问题是明白题目中目标函数的意义.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目