题目内容
向量a=(sinωx+cosωx,1),b=(f(x),sinωx),其中0<ω<1,且a∥b。将f(x)的图象沿x轴向左平移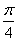 个单位,沿y轴向下平移
个单位,沿y轴向下平移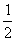 个单位,得到g(x)的图象,已知g(x)的图象关于
个单位,得到g(x)的图象,已知g(x)的图象关于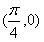 对称。
对称。
(1)求ω的值;
(2)求g(x)在[0,4π]上的单调递增区间。
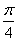 个单位,沿y轴向下平移
个单位,沿y轴向下平移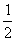 个单位,得到g(x)的图象,已知g(x)的图象关于
个单位,得到g(x)的图象,已知g(x)的图象关于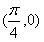 对称。
对称。(1)求ω的值;
(2)求g(x)在[0,4π]上的单调递增区间。
解:(1)∵a∥b
∴(cosωx+sinωx)sinωx-f(x)=0
∴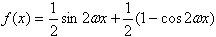
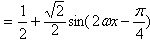
而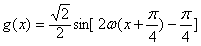 关于
关于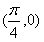 对称
对称
∴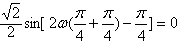
∴
∴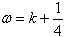 ,由k∈Z,0<ω<1得
,由k∈Z,0<ω<1得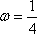 。
。
(2)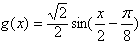
由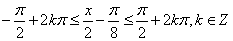
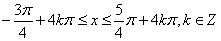
又∵0≤x≤4π,且k=0时,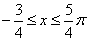
k=1时,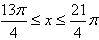
∴g(x)的单调递增区间: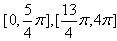 。
。
∴(cosωx+sinωx)sinωx-f(x)=0
∴
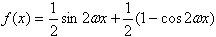
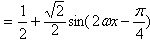
而
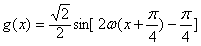 关于
关于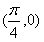 对称
对称∴
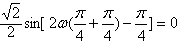
∴

∴
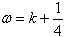 ,由k∈Z,0<ω<1得
,由k∈Z,0<ω<1得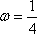 。
。(2)
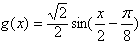
由
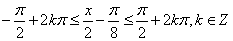
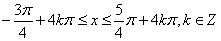
又∵0≤x≤4π,且k=0时,
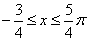
k=1时,
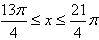
∴g(x)的单调递增区间:
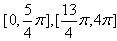 。
。
练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
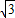 sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数
sinωx,cosωx),b=(cosωx,-cosωx),(ω>0),函数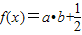 的图象的两相邻对称轴间的距离为
的图象的两相邻对称轴间的距离为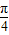 .
.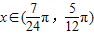 时,
时,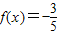 ,求cos4x的值;
,求cos4x的值;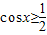 ,x∈(0,π),且f(x)=m有且仅有一个实根,求实数m的值.
,x∈(0,π),且f(x)=m有且仅有一个实根,求实数m的值.