题目内容
【题目】已知动点P到定点F(1，0)和到直线x＝2的距离之比为
，设动点P的轨迹为曲线E，过点F作垂直于x轴的直线与曲线E相交于A，B两点，直线l：y＝mx＋n与曲线E交于C，D两点，与线段AB相交于一点(与A，B不重合)．
(1)求曲线E的方程；
(2)当直线l与圆x2＋y2＝1相切时，四边形ABCD的面积是否有最大值？若有，求出其最大值及对应的直线l的方程；若没有，请说明理由．
【答案】见解析
【解析】
解：(1)设点P(x，y)，由题意可得，
＝
，
整理可得
＋y2＝1.
∴曲线E的方程是＋y2＝1.
(2)设C(x1，y1)，D(x2，y2)，由已知可得|AB|＝
.
当m＝0时，不合题意．
当m≠0时，由直线l与圆x2＋y2＝1相切，可得
＝1，即m2＋1＝n2.
联立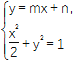
消去y得
x2＋2mnx＋n2－1＝0，
∴Δ＝4m2n2－4 (n2－1)＝2m2＞0，
则x1＝
，x2＝
，
∴S四边形ACBD＝
|AB||x2－x1|＝
＝
≤，
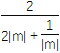当且仅当2|m|＝
，即m＝±时等号成立，此时n＝±
，经检验可知，直线y＝x－和直线y＝－x＋符合题意．
练习册系列答案
相关题目
【题目】葫芦岛市某高中进行一项调查：2012年至2016年本校学生人均年求学花销
（单位：万元）的数据如下表：
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代号 | 1 | 2 | 3 | 4 | 5 |
年求学花销 | 3.2 | 3.5 | 3.8 | 4.6 | 4.9 |
（1）求
关于
的线性回归方程；
（2）利用（1）中的回归方程，分析2012年至2016年本校学生人均年求学花销的变化情况，并预测该地区2017年本校学生人均年求学花销情况．
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
