题目内容
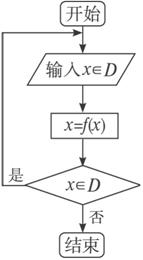
对于任意函数f(x),x∈D,可按图示构造一个数列发生器,其工作原理如下:
①输入数据x0∈D,经数列发生器输出x1=f(x0)；
②若x1
D,则数列发生器结束工作；若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.现在定义f(x)=
.
(1)若输入x0=
,则由数列发生器产生数列{xn}.请写出数列{xn}的所有项.
(2)若要数列发生器产生一个无穷的常数数列,试求输入的初始数据x0的值.
(3)若输入x0时,产生的无穷数列{xn}满足:对任意正整数n,均有xn＜xn+1,求x0的取值范围.
解析：(1)∵f(x)的定义域D=(-∞,-1)∪(-1,+∞),
∴ 数列xn只有三项:x1=
,x2=,x3=-1 .
(2)∵f(x)==x,即x2-3x+2=0,∴x=1或x=2,即当x0=1或2时,xn+1==xn.故当x0=1时,xn=1；当x0=2时,xn=2(n∈N*).
(3)解不等式x＜
,得x＜-1或1＜x＜2.要使x1＜x2,则x1＜-1或1＜x1＜2.
对于函数f(x)=
=4-
,
若x1＜-1,则x2=f(x1)＞4,x3=f(x2)＜x2.
当1＜x1＜2时,x2=f(x1)＞x1,且1＜x2＜2,依次类推可得数列{xn}的所有项均满足xn+1＞xn(n∈N*).
综上所述,x1∈(1,2).由x1=f(x0),得x0∈(1,2).
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
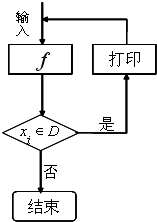12、对于任意函数f（x），x∈D，可构造一个数列发生器，其工作原理如下：
对于任意函数f（x），x∈D，可按如图所示构造一个数列发生器，其工作原理如下：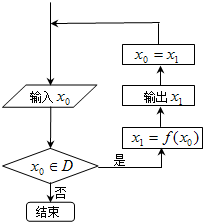
如图的发生器对于任意函数f（x），x∈D可制造出一系列的数据，其工作原理如下：①若输入数据x0∉D，则发生器结束工作；②若输入数据x0∈D，时，则发生器输出x1，其中x1=f（x0），并将x1反馈回输入端．现定义f（x）=2x+1，D=（0，50）．若输入x0=1，那么，当发生器结束工作时，输出数据的总个数为