题目内容
 12、对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下:
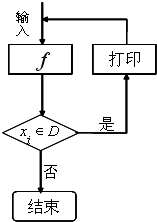
12、对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下:①输入数据x0∈D,经过数列发生器后输出x1=f(x0).
②若x1∉D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),并依此规律继续下去.现定义f(x)=2x+1,D=(0,1000),若输入x0=1,这样,当发生器结束工作时,输出数据的总个数为( )
分析:根据x1=f(x0)和x0=1,f(x)=2x+1,得到首项和递推式,用递推式代入首项做出第二项、第三项,以此类推得到符合条件D=(0,1000)的数据,数出个数,得到结论.
解答:解:依题意得x1=f(x0)=f(1)=3,
∵当n≥2时,若xn-1∈D,则输出xn=f(xn-1)
=2xn-1+1.
由此得到输出数据分别为:3,7,15,31,63,127,255,511,1023.
∴当发生器结束工作时,输出数据的总个数为9.
故选B
∵当n≥2时,若xn-1∈D,则输出xn=f(xn-1)
=2xn-1+1.
由此得到输出数据分别为:3,7,15,31,63,127,255,511,1023.
∴当发生器结束工作时,输出数据的总个数为9.
故选B
点评:本题是一个新定义问题,解题的关键是读懂题意,根据题目的条件变形整理,得到我们熟悉的数学知识,看懂题意以后,题目解起来不麻烦,因为他考查的不是运算,而是理解和实际应用.

练习册系列答案
相关题目
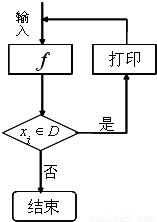
 对于任意函数f(x),x∈D,可按如图所示构造一个数列发生器,其工作原理如下:
对于任意函数f(x),x∈D,可按如图所示构造一个数列发生器,其工作原理如下: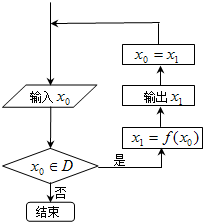 如图的发生器对于任意函数f(x),x∈D可制造出一系列的数据,其工作原理如下:①若输入数据x0∉D,则发生器结束工作;②若输入数据x0∈D,时,则发生器输出x1,其中x1=f(x0),并将x1反馈回输入端.现定义f(x)=2x+1,D=(0,50).若输入x0=1,那么,当发生器结束工作时,输出数据的总个数为
如图的发生器对于任意函数f(x),x∈D可制造出一系列的数据,其工作原理如下:①若输入数据x0∉D,则发生器结束工作;②若输入数据x0∈D,时,则发生器输出x1,其中x1=f(x0),并将x1反馈回输入端.现定义f(x)=2x+1,D=(0,50).若输入x0=1,那么,当发生器结束工作时,输出数据的总个数为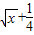 ,D=(0,+∞).若输入x=1,则打印输出的数据x20= .
,D=(0,+∞).若输入x=1,则打印输出的数据x20= .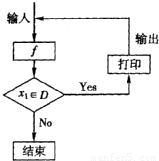
 对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下:
对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下: