题目内容
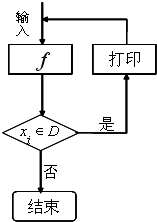
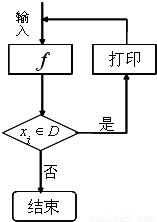
 对于任意函数f(x),x∈D,可按如图所示构造一个数列发生器,其工作原理如下:
对于任意函数f(x),x∈D,可按如图所示构造一个数列发生器,其工作原理如下:①输入数据x0∈D,经过数列发生器输出x1=f(x0);
②若x1∉D,则数列发生器结束工作;若x1∈D,则将x1反馈回输入端,再输出x2=f(x1),依此类推.
若f(x)=x+
| x |
| 1 |
| 4 |
121
121
.分析:根据程序,得到首项和递推式,从而可得{
}组成以
为首项,
为公差的等差数列,求出通项,即可得出结论.
| xn |
| 3 |
| 2 |
| 1 |
| 2 |
解答:解:依题意得x1=f(x0)=f(1)=
,
∵当n≥2时,若xn-1∈D,则输出xn=f(xn-1)=(
+
)2
∴
-
=
.
∴{
}组成以
为首项,
为公差的等差数列
∴
=
∴xn=(
)2
∴x20=121,
故答案为:121.
| 9 |
| 4 |
∵当n≥2时,若xn-1∈D,则输出xn=f(xn-1)=(
| xn-1 |
| 1 |
| 2 |
∴
| xn |
| xn-1 |
| 1 |
| 2 |
∴{
| xn |
| 3 |
| 2 |
| 1 |
| 2 |
∴
| xn |
| n+2 |
| 2 |
∴xn=(
| n+2 |
| 2 |
∴x20=121,
故答案为:121.
点评:本题是一个新定义问题,解题的关键是读懂题意,根据题目的条件变形整理,属于中档题.

练习册系列答案
相关题目
 12、对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下:
12、对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下: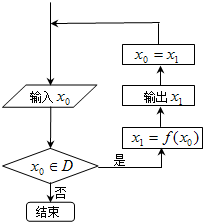 如图的发生器对于任意函数f(x),x∈D可制造出一系列的数据,其工作原理如下:①若输入数据x0∉D,则发生器结束工作;②若输入数据x0∈D,时,则发生器输出x1,其中x1=f(x0),并将x1反馈回输入端.现定义f(x)=2x+1,D=(0,50).若输入x0=1,那么,当发生器结束工作时,输出数据的总个数为
如图的发生器对于任意函数f(x),x∈D可制造出一系列的数据,其工作原理如下:①若输入数据x0∉D,则发生器结束工作;②若输入数据x0∈D,时,则发生器输出x1,其中x1=f(x0),并将x1反馈回输入端.现定义f(x)=2x+1,D=(0,50).若输入x0=1,那么,当发生器结束工作时,输出数据的总个数为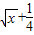 ,D=(0,+∞).若输入x=1,则打印输出的数据x20= .
,D=(0,+∞).若输入x=1,则打印输出的数据x20= .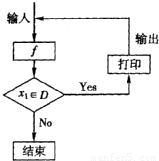
 对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下:
对于任意函数f(x),x∈D,可构造一个数列发生器,其工作原理如下: