Question

【题目】如图，长方体ABCD﹣A1B1C1D1中，AA1=AB=2，AD=1点E，F，G分别是DD1 ， AB，CC1的中点，则异面直线A1E与GF所成的角是（ ）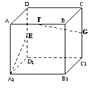
A.90°
B.60°
C.45°
D.30°

Answer 1

【答案】A
【解析】解：由题意：ABCD﹣A1B1C1D1是长方体，E，F，G分别是DD1 ， AB，CC1的中点，连接B1G， ∵A1E∥B1G，
∴∠FGB1为异面直线A1E与GF所成的角．
连接FB1 ，

在三角形FB1G中，AA1=AB=2，AD=1，
B1F= =
B1G= = ，
FG= = ，
B1F2=B1G2+FG2 ．
∴∠FGB1=90°，
即异面直线A1E与GF所成的角为90°．
故选A．
异面直线所成的角通过平移相交，找到平面角，转化为平面三角形的角求解，由题意：E，F，G分别是DD1 ， AB，CC1的中点，连接B1G，FB1 ， 那么∠FGB1就是异面直线A1E与GF所成的角．