题目内容
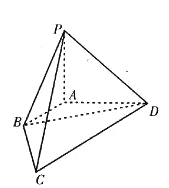
【题目】如图,在三棱锥A-BCD中,![]() ,点E为棱CD上的一点,且
,点E为棱CD上的一点,且![]() .
.
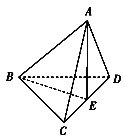
(1)求证:平面![]() 平面BCD;
平面BCD;
(2)若三棱锥A-BCD的体积为![]() ,求三棱锥E-ABD的高.
,求三棱锥E-ABD的高.
【答案】(1)见解析;(2)![]()
【解析】
(1)证明![]() ,
,![]() ,再证明
,再证明![]() 平面BCD得到答案.
平面BCD得到答案.
(2)计算![]() ,根据体积计算
,根据体积计算![]() ,判断点E为棱CD的中点,根据体积
,判断点E为棱CD的中点,根据体积![]() 计算得到答案.
计算得到答案.
(1)因为![]() ,所以
,所以![]() ,所以
,所以![]() .
.
因为![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面ADC,又
平面ADC,又![]() 平面ADC,所以
平面ADC,所以![]() .
.
又![]() ,所以
,所以![]() 平面BCD.
平面BCD.
因为![]() 平面ABE,所以平面
平面ABE,所以平面![]() 平面BCD.
平面BCD.
(2)因为![]() ,
,
所以![]() .
.
![]() 平面BCD,因为三棱锥A-BCD的体积为
平面BCD,因为三棱锥A-BCD的体积为![]() ,
,
所以![]() ,所以
,所以![]() ,
,
在![]() 中,
中,![]() ,所以点E为棱CD的中点.
,所以点E为棱CD的中点.
设三棱锥E-ABD的高为h,则点C到平面ABD的距离为2h,
所以![]() ,所以
,所以![]() ,
,
所以三棱锥E-ABD的高为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某乡镇为了打赢脱贫攻坚战,决定盘活贫困村的各项经济发展要素,实施了产业、创业、就业“三业并举”工程.在实施过程中,引导某贫困村农户因地制宜开展种植某经济作物.该类经济作物的质量以其质量指标值来衡量,质量指标值越大表明质量越好,记其质量指标值为![]() ,其质量指标的等级划分如下表1:
,其质量指标的等级划分如下表1:
表1
质量指标值 | 产品等级 |
| 优秀品 |
| 良好品 |
| 合格品 |
| 不合格品 |
为了解该类经济作物在当地的种植效益,当地引种了甲、乙两个品种.并随机抽取了甲、乙两个品种的各![]() 件产品,测量了每件产品的质量指标值,得到下面产品质量指标值频率分布直方图(图1和图2).
件产品,测量了每件产品的质量指标值,得到下面产品质量指标值频率分布直方图(图1和图2).
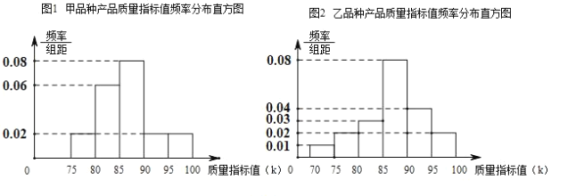
(1)若将频率视为概率,从乙品种产品中有放回地随机抽取![]() 件,记“抽出乙品种产品中至少
件,记“抽出乙品种产品中至少![]() 件良好品或以上”为事件
件良好品或以上”为事件![]() ,求事件
,求事件![]() 发生的概率
发生的概率![]() ;(结果保留小数点后
;(结果保留小数点后![]() 位)(参考数值:
位)(参考数值:![]() ,
,![]() )
)
(2)若甲、乙两个品种的销售利润率![]() 与质量指标值
与质量指标值![]() 满足表2
满足表2
表2
质量指标值 |
|
|
|
|
销售利润率 |
|
|
|
|
其中![]() ,试分析,从长期来看,种植甲、乙哪个品种的平均利润率较大?
,试分析,从长期来看,种植甲、乙哪个品种的平均利润率较大?
【题目】![]() 三个班共有
三个班共有![]() 名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):
名学生,为调查他们的上网情况,通过分层抽样获得了部分学生一周的上网时长,数据如下表(单位:小时):
|
|
|
|
|
|
(1)试估计![]() 班的学生人数;
班的学生人数;
(2)从这120名学生中任选1名学生,估计这名学生一周上网时长超过15小时的概率;
(3)从A班抽出的6名学生中随机选取2人,从B班抽出的7名学生中随机选取1人,求这3人中恰有2人一周上网时长超过15小时的概率.