题目内容
设平面向量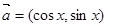 ,
,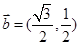 ,函数
,函数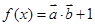 .
.
(Ⅰ)求函数 的值域和函数的单调递增区间;
的值域和函数的单调递增区间;
(Ⅱ)当 ,且
,且 时,求
时,求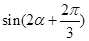 的值.
的值.
(Ⅰ)值域是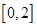 ;单调增区间为
;单调增区间为 ;(Ⅱ)
;(Ⅱ)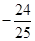
解析试题分析:根据 的特点,利用平面向量的数量积的运算法则化简,然后利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,从而确定出
的特点,利用平面向量的数量积的运算法则化简,然后利用两角和的正弦函数公式及特殊角的三角函数值化为一个角的正弦函数,从而确定出 的解析式,
的解析式,
根据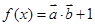 、数量积公式和三角函数恒等变换,求出
、数量积公式和三角函数恒等变换,求出
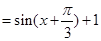 ,在根据正弦函数的性质求出函数
,在根据正弦函数的性质求出函数 的值域;
的值域;
②根据正弦函数的单调区间为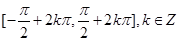 ,列出不等式,求出不等式的解集即可得到
,列出不等式,求出不等式的解集即可得到 的取值范围即为
的取值范围即为 的递增区间;
的递增区间;
③根据 ,代入
,代入 的解析式中,得到
的解析式中,得到 的值,根据
的值,根据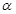 的范围求出
的范围求出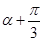 的范围,利用同角三角函数间的基本关系求出
的范围,利用同角三角函数间的基本关系求出 的值,把所求的式子利用二倍角的正弦函数公式化简,将
的值,把所求的式子利用二倍角的正弦函数公式化简,将 和
和 的值代入即可求出值.
的值代入即可求出值.
试题解析:依题意

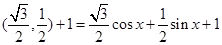 (2分)
(2分)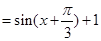 (4分)
(4分)
(Ⅰ) 函数 的值域是
的值域是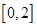 ; (5分)
; (5分)
令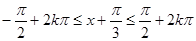 ,解得
,解得 (7分)
(7分)
所以函数 的单调增区间为
的单调增区间为 . (8分)
. (8分)
(Ⅱ)由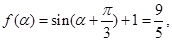 得
得 ,
,
因为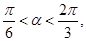 所以
所以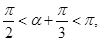 得
得 , (10分)
, (10分)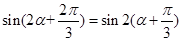

 (12分).
(12分).
考点:1.正弦函数的定义域和值域、正弦函数的单调性;2. 三角函数的恒等变换及化简求值;3.平面向量数量积的运算.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 sin2x+sin xcos x,x∈
sin2x+sin xcos x,x∈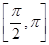 .
.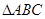 的三个内角,若向量
的三个内角,若向量 ,
, ,且
,且 .
.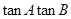 的值;
的值;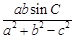 的最大值.
的最大值.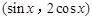 ,b=
,b=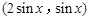 ,设函数
,设函数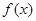 =a
=a b.
b. 的单调递增区间;
的单调递增区间;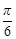 个单位,得到函数
个单位,得到函数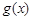 的图象,求函数
的图象,求函数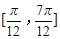 上的最大值和最小值.
上的最大值和最小值. sinxcosx-2cos2x+l.
sinxcosx-2cos2x+l. ∈(0,
∈(0, ),且f(
),且f( ,记函数
,记函数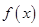 的最小正周期为
的最小正周期为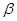 ,向量
,向量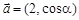 ,
, (
(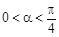 ),且
),且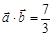 .
.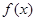 在区间
在区间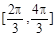 上的最值;
上的最值;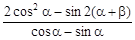 的值.
的值.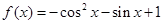 .
.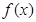 的最小值;
的最小值;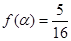 ,求
,求 的值.
的值. .
. 的最小正周期;
的最小正周期;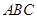 中,角
中,角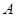 、
、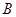 、
、 所对的边分别为
所对的边分别为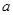 、
、 、
、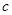 ,且
,且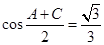 .
.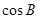 的值;
的值;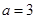 ,
,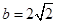 ,求
,求