题目内容
已知函数f(x)＝
sin2x＋sin xcos x，x∈
.
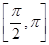(1)求f(x) 的零点；
(2)求f(x)的最大值和最小值．
（1）零点为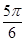
或π（2）最大值为，最小值为－1＋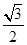
解析
练习册系列答案
唐印文化课时测评系列答案
导学与测试系列答案
相关题目
唐印文化课时测评系列答案导学与测试系列答案题目内容
已知函数f(x)＝sin2x＋sin xcos x，x∈.
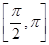(1)求f(x) 的零点；
(2)求f(x)的最大值和最小值．
（1）零点为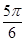或π（2）最大值为，最小值为－1＋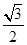
解析
唐印文化课时测评系列答案导学与测试系列答案
-φ)-sin(
,0)对称,且在区间[0,
． 的部分图象如图所示，其中点
是图象的一个最高点.
的解析式；
且
，求
．
，设函数
.
在
上的单调递增区间；
中，
，
，
分别是角
，
，
的对边，
，
，
，求边
（A＞0，
＞0，
）的图象的一部分如下图所示.
（－6，2）时，求函数g（x）= f（x＋2）的单调递增区间.
处取得最大值2，其图象与x轴的相邻两个交点的距离为
.
的值域．
sin ωx·cos ωx＋cos 2ωx－
(ω>0)，其最小正周期为
.
个单位，再将图象上各点的横坐标伸长到原来的2倍(纵坐标不变)，得到函数y＝g(x)的图象，若关于x的方程g(x)＋k＝0，在区间
上有且只有一个实数解，求实数k的取值范围．
，
，函数
.
的值域和函数的单调递增区间; 
,且
时,求
的值.
＝1，求6sinx＋4tan2x－3cos2(π－x)的值．