题目内容
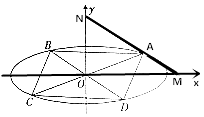
【题目】如图所示,已知正方体ABCD-A1B1C1D1的棱长为a , 过点B1作B1E⊥BD1于点E , 求A、E两点之间的距离.
【答案】解:以D为坐标原点建立如图所示的空间直角坐标系,
根据题意,可得A(a,0,0)、B(a,a,0)、D1(0,0,a)、B1(a,a,a).
过点E作EF⊥BD于F,如图所示,
则在Rt△BB1D1中,
|BB1|=a,|BD1|= ![]() a,|B1D1|=
a,|B1D1|= ![]() a,
a,
所以|B1E|= ![]() ,
,
所以Rt△BEB1中,|BE|= ![]() a
a
由Rt△BEF∽Rt△BD1D,得|BF|= ![]() a,|EF|=
a,|EF|= ![]() ,所以点F的坐标为(
,所以点F的坐标为( ![]() ,0),
,0),
则点E的坐标为( ![]() ,
, ![]() ).
).
由两点间的距离公式,得
|AE|= ![]() =
= ![]() a,
a,
所以A、E两点之间的距离是 ![]() a.
a.
【解析】先建立适当的直角坐标系,根据题意表示出相关点的坐标,再根据题中点E的位置关系求得点E的坐标,利用两点间的距离公式表示出线段AE的长度.

【题目】已知圆O1的方程为x2+(y+1)2=4,圆O2的圆心为O2(2,1).
(1)若圆O1与圆O2外切,求圆O2的方程;
(2)若圆O1与圆O2交于A , B两点,且|AB|=2 ![]() ,求圆O2的方程.
,求圆O2的方程.
【题目】二手车经销商小王对其所经营的某一型号二手汽车的使用年数x(0<x≤10)与销售价格y(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
参考公式: 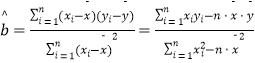 ,
, ![]() .
.
(1)若这两个变量呈线性相关关系,试求y关于x的回归直线方程 ![]() ;
;
(2)已知小王只收购使用年限不超过10年的二手车,且每辆该型号汽车的收购价格为ω=0.03x2﹣1.81x+16.2万元,根据(1)中所求的回归方程,预测x为何值时,小王销售一辆该型号汽车所获得的利润L(x)最大? (销售一辆该型号汽车的利润=销售价格﹣收购价格)