题目内容

【题目】如图，在三棱锥P-ABC中， 且底面，D是PC的中点，已知,AB=2，AC=,PA=2.

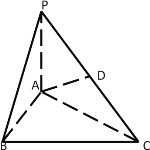
（1）求三棱锥P-ABC的体积

（2）求异面直线BC与AD所成角的余弦值。

【答案】（1）；（2）.

【解析】

(1)先求出的面积，结合底面,利用锥体的体积公式能求出三棱锥的体积；(2)取中点，连接，则是异面直线与所成的角（或其补角），根据余弦定理能求出异面直线与所成角的余弦值.

(1)∵在三棱锥PABC中,PA⊥底面ABC,D是PC的中点

∠BAC= ，AB=2，AC=，PA=2.∴，

∴三棱锥PABC的体积为

(2)如图,取PB的中点E,连接DE,AE,则ED∥BC，

∴∠ADE或其补角是异面直线BC与AD所成的角.

在△ADE中,，

中，

故:异面直线BC与AD所成角的余弦值为．

练习册系列答案
相关题目

【题目】已知圆M过C(1,-1),D(-1,1)两点，且圆心M在x+y-2=0上．

（1）求圆M的方程；

（2）设点P是直线3x+4y+8=0上的动点，PA,PB是圆M的两条切线，A,B为切点，求四边形PAMB面积的最小值．

【题目】已知椭圆和双曲线有共同焦点，是它们的一个交点，，记椭圆和双曲线的离心率分别，则的最小值是（ ）

A. B. C. D.

【题目】已知函数f（x）=ax2﹣ax﹣xlnx，且f（x）≥0．
（Ⅰ）求a；
（Ⅱ）证明：f（x）存在唯一的极大值点x0 ， 且e﹣2＜f（x0）＜2﹣2 ．

【题目】已知函数f（x）=2sin（ωx+φ）+1（ω＞0，|φ|≤ ），其图象与直线y=﹣1相邻两个交点的距离为π，若f（x）＞1对x∈（﹣ ， ）恒成立，则φ的取值范围是（ ）
A.
B.
C.
D.

【题目】棱长为1的正方体中，分别是的中点.

①在直线上运动时，三棱锥体积不变；

②在直线上运动时，始终与平面平行；

③平面平面；

④连接正方体的任意的两个顶点形成一条直线，其中与棱所在直线异面的有条；

其中真命题的编号是_______________.（写出所有正确命题的编号）

【题目】设函数f（x）是定义在R上的偶函数，且对任意的x∈R，都有f（x+1）=f（x﹣1），已知当x∈[0，1]时，f（x）=2x﹣1 ， 有以下结论：
①2是函数f（x）的一个周期；
②函数f（x）在（1，2）上单调递减，在（2，3）上单调递增；
③函数f（x）的最大值为1，最小值为0；
④当x∈（3，4）时，f（x）=23﹣x ．
其中，正确结论的序号是 ． （请写出所有正确结论的序号）

【题目】如图，在正方体中，是的中点．

(1)求证：平面；

(2)求异面直线和所成角的大小．

【题目】已知函数f（x）=x2﹣ax﹣alnx（a∈R），g（x）=﹣x3+ x2+2x﹣6，g（x）在[1，4]上的最大值为b，当x∈[1，+∞）时，f（x）≥b恒成立，则a的取值范围（ ）
A.a≤2
B.a≤1
C.a≤﹣1
D.a≤0

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网