题目内容
13、函数f(x)=lg(x2-2ax+1+a)在区间(-∞,1]上单调递减,则实数a的取值范围是
[1,2)
.分析:复合函数f(x)=lg(x2-2ax+1+a)中,对数函数y=lgx为单调递增,在区间(-∞,1]上,a的取值需令真数x2-2ax+1+a>0,且函数u=x2-2ax+1+a在区间(-∞,1]上应单调递减,这样复合函数才能单调递减.
解答:解:令u=x2-2ax+1+a,则f(u)=lgu,
配方得u=x2-2ax+1+a=(x-a)2 -a2+a+1,故对称轴为x=a
如图所示: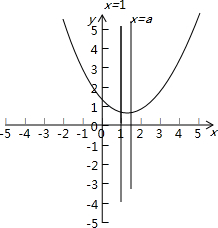
由图象可知当对称轴a≥1时,u=x2-2ax+1+a在区间(-∞,1]上单调递减,
又真数x2-2ax+1+a>0,二次函数u=x2-2ax+1+a在(-∞,1]上单调递减,故只需当x=1时,若x2-2ax+1+a>0,则x∈(-∞,1]时,真数x2-2ax+1+a>0,
代入x=1解得a<2,所以a的取值范围是[1,2)
故答案为:[1,2)
配方得u=x2-2ax+1+a=(x-a)2 -a2+a+1,故对称轴为x=a
如图所示:

由图象可知当对称轴a≥1时,u=x2-2ax+1+a在区间(-∞,1]上单调递减,
又真数x2-2ax+1+a>0,二次函数u=x2-2ax+1+a在(-∞,1]上单调递减,故只需当x=1时,若x2-2ax+1+a>0,则x∈(-∞,1]时,真数x2-2ax+1+a>0,
代入x=1解得a<2,所以a的取值范围是[1,2)
故答案为:[1,2)
点评:y=f[g(x)]型函数可以看作由两个函数y=f(u)和u=g(x)复合而成,一般称其为复合函数.其中y=f(u)为外层函数,u=g(x)为内层函数.若内、外层函数的增减性相同,则复合函数为增函数;若内、外层函数的增减性相反,则复合函数为减函数.即复合函数单调性遵从同增异减的原则.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目