题目内容
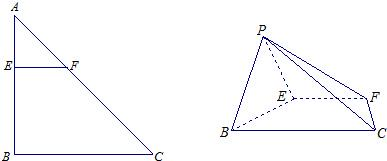
如图1,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.


图1 图2
(1)求证:A1C⊥平面BCDE;
(2)过点E作截面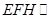 平面
平面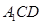 ,分别交CB于F,
,分别交CB于F,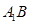 于H,求截面
于H,求截面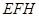 的面积;
的面积;
(3)线段BC上是否存在点P,使平面A1DP与平面A1BE成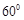 的角?说明理由.
的角?说明理由.
【答案】
(1)要证明线面垂直,则根据线面垂直的判定定理来得到。(2)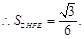
(3) 存在线段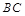 上存在点
上存在点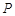 ,使平面
,使平面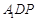 与平面
与平面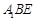 成
成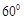 的角
的角
【解析】
试题分析:解: (1)
(1)
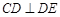 ,
,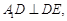
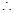
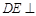 平面
平面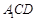 .
.
又
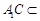 平面
平面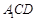 ,
, 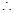
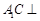
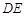 .
.
又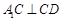 ,
, 
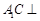 平面
平面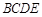 ……4分
……4分
(2) )过点E作EF∥CD交BC于F,过点F作FH∥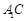 交
交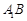 于H,连结EH.
于H,连结EH.
则截面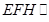 平面
平面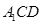 。
。
因为四边形EFCD为矩形,所以EF=CD=1,CF=DE=4,从而FB=2,HF=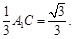
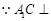 平面
平面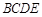 , FH∥
, FH∥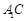 ,
,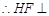 平面
平面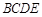 ,
,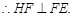
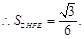 ……8分
……8分
(3)假设线段BC上存在点P,使平面A1DP与平面A1BE成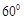 的角。
的角。
设 点坐标为
点坐标为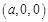 ,则
,则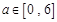 .
.
如图建系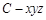 ,则
,则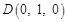 ,
,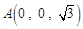 ,
,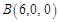 ,
,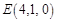 .
.

∴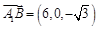 ,
,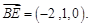
设平面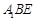 法向量为
法向量为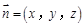 ,
,
则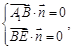
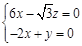 ∴
∴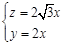 ,∴
,∴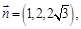
设平面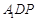 法向量为
法向量为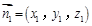 ,因为
,因为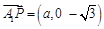 ,
,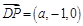 .
.
则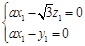 ∴
∴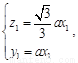 ∴
∴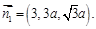
则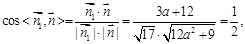 ∴56
∴56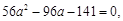 ,
,
解得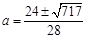
∵ ∴
∴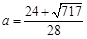
所以存在线段 上存在点
上存在点 ,使平面
,使平面 与平面
与平面 成
成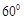 的角. ……12分
的角. ……12分
考点:空间中点线面的位置关系的运用
点评:解决的关键是根据面面垂直化的判定定理以及二面角的概念来求解,属于基础题。

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.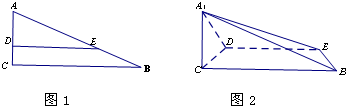 如图,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2.
如图,在Rt△ABC中,∠C=90°,BC=6,AC=3,D,E分别是AC,AB上的点,且DE∥BC,DE=4,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图2. (2009•普陀区一模)如图,在 Rt△AOB中,
(2009•普陀区一模)如图,在 Rt△AOB中,