题目内容
如图,在Rt△ABC中,AB=BC=4,点E、F分别在线段AB、AC上,且EF∥BC,将△AEF沿EF折起到△PEF的位置,使得二面角P-EF-B的大小为60°.(1)求证:EF⊥PB;
(2)当点E为线段AB的中点时,求PC与平面BCFE所成角的大小.
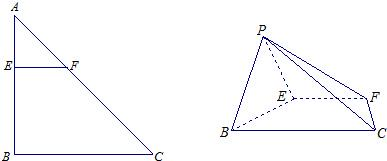
分析:(1)欲证EF⊥PB,可先证EF⊥平面PEB,根据直线与平面垂直的判定定理可知只需证EF与平面PEB内两相交直线垂直,而EF⊥EB,EF⊥EP,EB∩EP=E,满足定理条件;
(2)过点P作PD⊥EB交EB于D,连接DC,根据线面所成角的定义可知∠PCD是PC与平面BCFE所成的角,根据∠PEB是二面角P-EF-B的平面角求出PD,在Rt△PCD中求出此角正切值即可.
(2)过点P作PD⊥EB交EB于D,连接DC,根据线面所成角的定义可知∠PCD是PC与平面BCFE所成的角,根据∠PEB是二面角P-EF-B的平面角求出PD,在Rt△PCD中求出此角正切值即可.
解答:解:(1)证明:在Rt△ABC中,EF∥BC,
∴EF⊥AB.
∴EF⊥EB,EF⊥EP.
又∵EB∩EP=E,
∴EF⊥平面PEB.
又∵PB?平面PEB,
∴EF⊥PB.
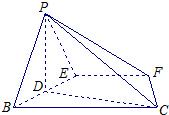 (2)过点P作PD⊥EB交EB于D,连接DC.
(2)过点P作PD⊥EB交EB于D,连接DC.
∵EF⊥平面PEB,PD?平面PEB,
∴EF⊥PD.
∵EF∩EB=E,
∴PD⊥平面BCFE.
∴CD是PC在平面BCFE内的射影.
∴∠PCD是PC与平面BCFE所成的角.
∵点E为线段AB的中点,AB=BC=4,
∴PE=EB=2.
∵EF⊥EB,EF⊥EP,
∴∠PEB是二面角P-EF-B的平面角.
∵二面角P-EF-B的大小为60°,
∴∠PEB=60°.
在Rt△PDE中,PD=PE•sin60°=
,DE=PE•cos60°=1
∴BD=1.
在Rt△DBC中,DC=
=
.
∴在Rt△PCD中,tan∠PCD=
=
.
∴PC与平面BCFE所成角的大小为arctan
.
∴EF⊥AB.
∴EF⊥EB,EF⊥EP.
又∵EB∩EP=E,
∴EF⊥平面PEB.
又∵PB?平面PEB,
∴EF⊥PB.
 (2)过点P作PD⊥EB交EB于D,连接DC.
(2)过点P作PD⊥EB交EB于D,连接DC.∵EF⊥平面PEB,PD?平面PEB,
∴EF⊥PD.
∵EF∩EB=E,
∴PD⊥平面BCFE.
∴CD是PC在平面BCFE内的射影.
∴∠PCD是PC与平面BCFE所成的角.
∵点E为线段AB的中点,AB=BC=4,
∴PE=EB=2.
∵EF⊥EB,EF⊥EP,
∴∠PEB是二面角P-EF-B的平面角.
∵二面角P-EF-B的大小为60°,
∴∠PEB=60°.
在Rt△PDE中,PD=PE•sin60°=
| 3 |
∴BD=1.
在Rt△DBC中,DC=
| 12+42 |
| 17 |
∴在Rt△PCD中,tan∠PCD=
| PD |
| DC |
| ||
| 17 |
∴PC与平面BCFE所成角的大小为arctan
| ||
| 17 |
点评:本题主要考查了直线与平面所成的角,以及二面角及其度量,考查空间想象能力、运算能力和推理论证能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2
如图,在Rt△ABC中,∠C=90°,D为BC上一点,∠DAC=30°,BD=2,AB=2| 3 |
A、2
| ||||
| B、3 | ||||
C、
| ||||
D、
|
 如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )
如图,在Rt△ABC中,AC=1,BC=x,D是斜边AB的中点,将△BCD沿直线CD翻折,若在翻折过程中存在某个位置,使得CB⊥AD,则x的取值范围是( )A、(0,
| ||||
B、(
| ||||
C、(
| ||||
| D、(2,4] |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E. 如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P.
如图,在Rt△ABC中,∠ABC=90°,BA=BC=2,AE⊥平面ABC,CD⊥平面ABC,CE交AD于点P. 8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=
8.如图,在Rt△ABC中,∠CAB=90°,AB=2,AC=