Question

(本题满分14分) 设向量α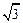＝(sin 2x，sin x＋cos x)，β＝(1，sin x－cos x)，其中x∈R，函数f(x)＝αβ．
(Ⅰ) 求f(x)的最小正周期；
(Ⅱ) 若f(θ)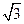＝，其中0＜θ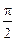＜，求cos(θ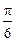＋)的值．

Answer 1

(Ⅰ)解：由题意得  f(x)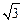＝sin 2x＋(sin x－cos x)(sin x＋cos x)
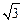＝sin 2x－cos 2x＝2sin (2x－)，
故f(x)的最小正周期T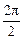＝＝π．                           
(Ⅱ)解：若f(θ)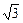＝，则2sin (2θ－)＝，
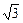所以，sin (2θ－)＝．
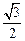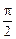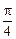又因为0＜θ＜，所以θ＝或．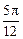
当θ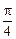＝时，cos(θ＋)＝cos(＋)＝；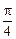
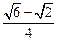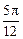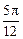当θ＝时，cos(θ＋)＝cos(＋)＝－cos＝－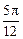

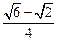
解析