题目内容
设函数 在
在 处取得极大值.
处取得极大值.(Ⅰ)求φ的值;
(Ⅱ)在△ABC中,a,b,c分别是A,B,C的对边且
 ,求A.
,求A.
【答案】分析:(Ⅰ)先将函数化简,再利用函数在 处取得极大值,及
处取得极大值,及 ,可求φ的值;
,可求φ的值;
(Ⅱ)利用(Ⅰ),可得 ,结合角A的范围,可求角A.
,结合角A的范围,可求角A.
解答:解:(Ⅰ)f(x)=sinx+cosx•sinφ-sinx•(1-cosφ)=cosx•sinφ+sinx•cosφ=sin(x+φ)
由 ,可得
,可得
∵ ,∴
,∴
(Ⅱ)由 ,可得
,可得
∵
∴
∴
∴
∴
点评:本题考查函数的化简,考查三角函数的性质,解题的关键是确定角的范围.
 处取得极大值,及
处取得极大值,及 ,可求φ的值;
,可求φ的值;(Ⅱ)利用(Ⅰ),可得
 ,结合角A的范围,可求角A.
,结合角A的范围,可求角A.解答:解:(Ⅰ)f(x)=sinx+cosx•sinφ-sinx•(1-cosφ)=cosx•sinφ+sinx•cosφ=sin(x+φ)
由
 ,可得
,可得
∵
 ,∴
,∴
(Ⅱ)由
 ,可得
,可得
∵

∴

∴

∴

∴

点评:本题考查函数的化简,考查三角函数的性质,解题的关键是确定角的范围.

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 在
在 处取得极大值或极小值,则称
处取得极大值或极小值,则称 为函数
为函数 是实数,1和
是实数,1和 是函数
是函数 的两个极值点.
的两个极值点. 和
和 的值;
的值; 的导函数
的导函数 ,求
,求 ,其中
,其中 ,求函数
,求函数 的零点个数.
的零点个数. 的函数
的函数 ,其中
,其中 为
为 上的常数,若函数
上的常数,若函数 在
在 处取得极大值
处取得极大值 .
. 有两个交点,求实数
有两个交点,求实数 的取值范围;
的取值范围; ,若对任意地
,若对任意地 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 在
在 处取得极大值,求函数
处取得极大值,求函数 ,
, ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.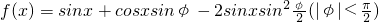 在
在 处取得极大值.
处取得极大值.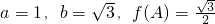 ,求A.
,求A.