题目内容
若函数 在
在 处取得极大值或极小值,则称
处取得极大值或极小值,则称 为函数
为函数 的极值点。
的极值点。
已知 是实数,1和
是实数,1和 是函数
是函数 的两个极值点.
的两个极值点.
(1)求 和
和 的值;
的值;
(2)设函数 的导函数
的导函数 ,求
,求 的极值点;
的极值点;
(3)设 ,其中
,其中 ,求函数
,求函数 的零点个数.
的零点个数.
(1)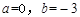 。 (2)
。 (2)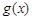 的极值点是-2 (3)当
的极值点是-2 (3)当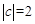 时,函数
时,函数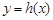 有5 个零点;当
有5 个零点;当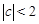 时,函数
时,函数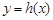 有9 个零点。
有9 个零点。
【考点】函数的概念和性质,导数的应用。
【解析】(1)求出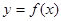 的导数,根据1和
的导数,根据1和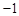 是函数
是函数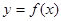 的两个极值点代入列方程组求解即可。
的两个极值点代入列方程组求解即可。
(2)由(1)得,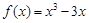 ,求出
,求出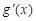 ,令
,令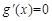 ,求解讨论即可。
,求解讨论即可。
(3)比较复杂,先分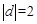 和
和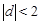 讨论关于
讨论关于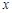 的方程
的方程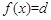 根的情况;再考虑函数
根的情况;再考虑函数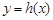 的零点
的零点
解:(1)由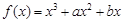 ,得
,得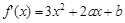 。
。
∵1和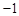 是函数
是函数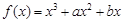 的两个极值点,
的两个极值点,
∴ 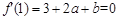 ,
,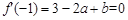 ,解得
,解得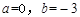 。
。
(2)∵ 由(1)得,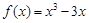 ,
,
∴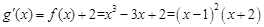 ,解得
,解得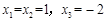 。
。
∵当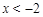 时,
时,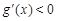 ;当
;当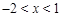 时,
时,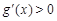 ,
,
∴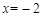 是
是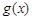 的极值点。
的极值点。
∵当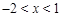 或
或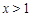 时,
时,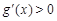 ,∴
,∴ 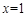 不是
不是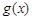 的极值点。
的极值点。
∴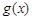 的极值点是-2。
的极值点是-2。
(3)令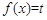 ,则
,则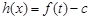 。
。
先讨论关于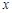 的方程
的方程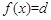 根的情况:
根的情况: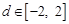
当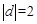 时,由(2 )可知,
时,由(2 )可知,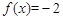 的两个不同的根为I 和一2 ,注意到
的两个不同的根为I 和一2 ,注意到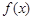 是奇函数,∴
是奇函数,∴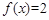 的两个不同的根为一和2。
的两个不同的根为一和2。
当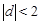 时,∵
时,∵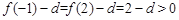 ,
,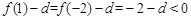 ,
,
∴一2 , -1,1 ,2 都不是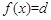 的根。
的根。
由(1)知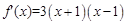 。
。
① 当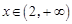 时,
时,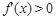 ,于是
,于是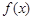 是单调增函数,从而
是单调增函数,从而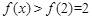 。
。
此时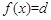 在
在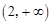 无实根。
无实根。
② 当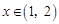 时.
时.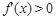 ,于是
,于是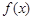 是单调增函数。
是单调增函数。
又∵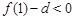 ,
,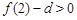 ,
,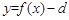 的图象不间断,
的图象不间断,
∴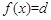 在(1 , 2 )内有唯一实根。
在(1 , 2 )内有唯一实根。
同理,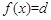 在(一2 ,一I )内有唯一实根。
在(一2 ,一I )内有唯一实根。
③ 当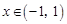 时,
时,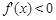 ,于是
,于是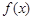 是单调减两数。
是单调减两数。
又∵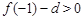 ,
, 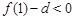 ,
,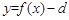 的图象不间断,
的图象不间断,
∴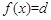 在(一1,1 )内有唯一实根。
在(一1,1 )内有唯一实根。
因此,当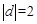 时,
时,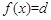 有两个不同的根
有两个不同的根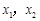 满足
满足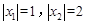 ;当
;当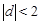 时
时
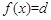 有三个不同的根
有三个不同的根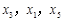 ,满足
,满足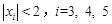 。
。
现考虑函数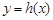 的零点:
的零点:
( i )当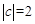 时,
时,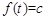 有两个根
有两个根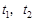 ,满足
,满足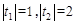 。
。
而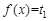 有三个不同的根,
有三个不同的根,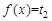 有两个不同的根,故
有两个不同的根,故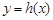 有5 个零点。
有5 个零点。
( 11 )当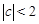 时,
时,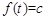 有三个不同的根
有三个不同的根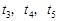 ,满足
,满足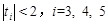 。
。
而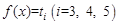 有三个不同的根,故
有三个不同的根,故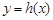 有9 个零点。
有9 个零点。
综上所述,当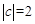 时,函数
时,函数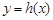 有5 个零点;当
有5 个零点;当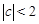 时,函数
时,函数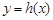 有9 个零点
有9 个零点

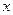 的函数
的函数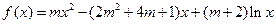 ,其中
,其中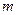 为
为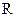 上的常数,若函数
上的常数,若函数 在
在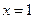 处取得极大值
处取得极大值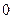
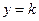 有两个交点,求实数
有两个交点,求实数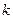 的取值范围
的取值范围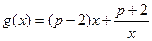 ,若对任意的
,若对任意的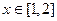 ,
,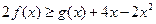 恒成立,求实数
恒成立,求实数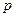 的取值范围.
的取值范围.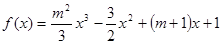
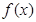 在
在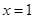 处取得极大值,求函数
处取得极大值,求函数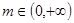 ,不等式
,不等式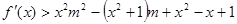 恒成立,求
恒成立,求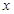 的取值范围
的取值范围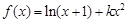 (
(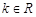 ).
).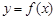 在
在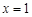 处取得极大值,求
处取得极大值,求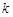 的值;
的值;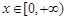 时,函数
时,函数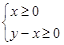 所表示的区域内,求
所表示的区域内,求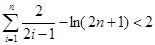 ,
,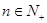 .
. 的函数
的函数 ,其中
,其中 为
为 上的常数,若函数
上的常数,若函数 在
在 处取得极大值
处取得极大值 .
. 有两个交点,求实数
有两个交点,求实数 的取值范围;
的取值范围; ,若对任意地
,若对任意地 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
 在
在 处取得极大值,求函数
处取得极大值,求函数 ,
, ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.