题目内容
已知O,A,M,B为平面上不同的四点,且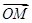 =λ
=λ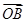 +(1-λ)
+(1-λ)  ,λ∈(1,2),则( ).
,λ∈(1,2),则( ).
| A.点M在线段AB上 |
| B.点B在线段AM上 |
| C.点A在线段BM上 |
| D.O,A,M,B四点共线 |
B
解析

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
在直角三角形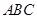 中,
中,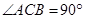 ,
,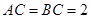 ,点
,点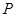 是斜边
是斜边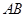 上的一个三等分点,则
上的一个三等分点,则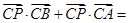 ( )
( )
| A.0 | B.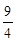 | C.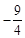 | D.4 |
在平行四边形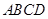 中,
中,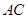 与
与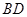 交于点
交于点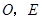 是线段
是线段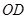 的中点,
的中点,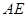 的延长线与
的延长线与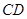 交于点
交于点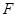 .若
.若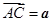 ,
,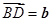 ,则
,则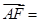 ( )
( )
A.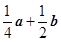 | B.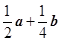 | C. | D. |
在平面直角坐标系中,已知向量 若
若 ,则x=( )
,则x=( )
| A.-2 | B.-4 | C.-3 | D.-1 |
点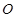 是平面
是平面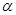 内的定点,点
内的定点,点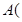 与点
与点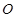 不同)的“对偶点”
不同)的“对偶点”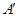 是指:点
是指:点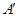 在射线
在射线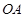 上且
上且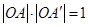 厘米
厘米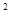 .若平面
.若平面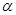 内不同四点
内不同四点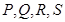 在某不过点O的直线
在某不过点O的直线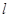 上,则它们相应的“对偶点”
上,则它们相应的“对偶点”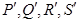 在
在
A.一个过点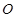 的圆上 的圆上 | B.一个不过点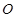 的圆上 的圆上 |
C.一条过点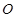 的直线上 的直线上 | D.一条不过点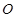 的直线上 的直线上 |
已知点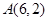 ,
,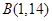 ,则与
,则与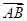 共线的单位向量为( )
共线的单位向量为( )
A.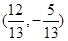 或 或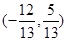 | B. |
C.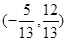 或 或 | D.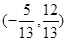 |
已知直线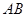 与抛物线
与抛物线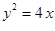 交于
交于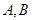 两点,
两点,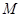 为
为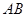 的中点,
的中点,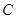 为抛物线上一个动点,若
为抛物线上一个动点,若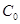 满足
满足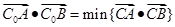 ,则下列一定成立的是( )。
,则下列一定成立的是( )。
A.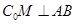 | B.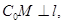 其中 其中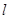 是抛物线过 是抛物线过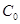 的切线 的切线 |
C.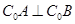 | D.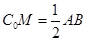 |
若向量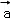 =(1,2),
=(1,2),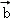 =(1,﹣1),则2
=(1,﹣1),则2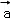 +
+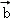 与
与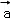
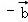 的夹角等于( )
的夹角等于( )
A.﹣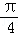 | B.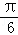 | C.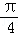 | D.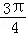 |
已知向量a=(2,1),a·b=10,|a+b|=5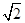 ,则|b|等于( ).
,则|b|等于( ).
A.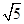 | B.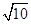 | C.5 | D.25 |