题目内容
18．
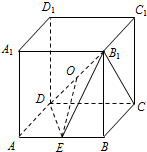如图，在正方体ABCD-A1B1C1D1中，O，E分别为B1D，AB的中点．（1）求证：OE∥平面BCC1B1；
（2）求证：OE⊥面B1DC．
分析 （1）连接BC1，设BC1∩B1C=F，连接OF，由于O，F分别是B1D与B1C的中点，利用三角形中位线定理可得，即四边形OEBF是平行四边形，可得OE∥BF，再利用线面平行的判定定理即可得出．
（2）由DC⊥面BCC1B1，可得BC1⊥DC，又可得BC1⊥面B1DC，而BC1∥OE，即可证明．
解答 
证明：（1）连接BC1，设BC1∩B1C=F，连接OF，
∵O，F分别是B1D与B1C的中点，
∴OF∥DC，
又E为AB中点，∴EB∥DC，
∴四边形OEBF是平行四边形，
∴OE∥BF，
又OE?面BCC1B1，BF?面BCC1B1，
∴OE∥面BCC1B1．
（2）∵DC⊥面BCC1B1，BC1?面BCC1B1，
∴BC1⊥DC，
又BC1⊥B1C，且DC，B1C?面B1DC，DC∩B1C=C，
∴BC1⊥面B1DC，
而BC1∥OE，∴OE⊥面B1DC．
点评 本题考查了空间线面位置关系、三角形中位线定理、平行四边形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
10．若点（4，tanθ）在函数y=log2x的图象上，则2cos2θ=（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{1}{5}$ | C． | $\frac{1}{2}$ | D． | $\frac{3}{5}$ |
7．已知集合P={x|1＜x≤2}，Q={x|x2+x-2≤0}，那么P∩Q等于（ ）
| A． | ∅ | B． | {1} | C． | {x|-2≤x≤2} | D． | {x|1＜x≤2} |