椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1的左右焦点为F1.F2.若C上存在一点P.使得|PF1|=2|PF2|.则C的离心率的范围是$[\frac{1}{3}.1)$．题目和参考答案——青夏教育精英家教网—

题目内容

14．椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点为F₁、F₂，若C上存在一点P，使得|PF₁|=2|PF₂|，则C的离心率的范围是$[\frac{1}{3}，1）$．

分析设P点的横坐标为x，根据|PF₁|=2|PF₂|，利用椭圆的第二定义，可得x关于e的表达式，进而根据x的范围确定e的范围．

解答解：设P点的横坐标为x
∵|PF₁|=2|PF₂|，
∴根据椭圆的第二定义，可得a+ex=2（a-ex）
∴3ex=a
∵x≤a，∴ex≤ea
∴$\frac{1}{3}$a≤ea，∴e≥$\frac{1}{3}$
∵0＜e＜1，∴e∈$[\frac{1}{3}，1）$．
故答案为：$[\frac{1}{3}，1）$．

点评本题主要考查了椭圆的简单性质，考查了椭圆的第二定义的灵活运用，属于基础题．

练习册系列答案

相关题目

7．若${∫}_{0}^{1}$（x²+mx）dx=0，则实数m的值为（　　）

6．设a＞0，b＞0，函数f（x）=ax²-bx-a+b．
（Ⅰ）（i）求不等式f（x）＜f（1）的解集；
（ii）若f（x）在[0，1]上的最大值为b-a，求$\frac{b}{a}$的取值范围；
（Ⅱ）当x∈[0，m]时，对任意的正实数a，b，不等式f（x）≤（x+1）|2b-a|恒成立，求实数m的最大值．

2．在等差数列{a_n}中，a₄+a₈=16，则a₃+a₆+a₉=（　　）

9．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的离心率e=$\frac{1}{2}$，F₁、F₂分别为左右焦点，点$M（2，\sqrt{3}）$与F₁连线段的垂直平分线恰好经过点F₂．
（Ⅰ）求椭圆C的方程；
（Ⅱ）过坐标原点O作不与坐标轴重合的直线l交椭圆C于P、Q两点，过P作x轴的垂线，垂足为D，连接QD并延长交椭圆C于点E，求证：直线PE与l的斜率的乘积是定值-$\frac{3}{2}$．

19．函数y=$\frac{1}{2}sinx+\frac{\sqrt{3}}{2}cosx（x∈[0，\frac{π}{2}]）$的单调递增区间是[0，$\frac{π}{6}$]．

6．已知F₁、F₂分别是双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$的左、右焦点，P为双曲线右支上的任意一点且$\frac{{|P{F_1}{|^2}}}{{|P{F_2}|}}=8a$，则双曲线离心率的取值范围是（　　）

	A．	命题“若a＞b＞0，则$\frac{1}{a}$＜$\frac{1}{b}$”的逆命题是真命题
	B．	命题p：?x∈R，x²-x+1＞0，则￢p：?x₀∈R，x₀²-x₀+1＜0
	C．	“a＞1，b＞1”是“ab＞1”成立的充分条件
	D．	“a＞b”是“a²＞b²”成立的充分不必要条件

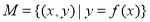已知集合，若对于任意，存在，使得成立，则称集合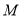是“理想集合”.给出下列4个集合：

①；

②；

③；

④.

其中所有“理想集合”的序号是（）

A.①③ B.②③

C.②④ D.③④

试题分类