题目内容
2.观察等式:$f(\frac{1}{3})+f(\frac{2}{3})=1,f(\frac{1}{4})+f(\frac{2}{4})+f(\frac{3}{4})=\frac{3}{2},f(\frac{1}{5})+f(\frac{2}{5})+f(\frac{3}{5})+f(\frac{4}{5})=2,f(\frac{1}{6})+f(\frac{2}{6})+f(\frac{3}{6})+f(\frac{4}{6})+f(\frac{5}{6})=\frac{5}{2}$,…由以上几个等式的规律可猜想$f(\frac{1}{2015})+f(\frac{2}{2015})+f(\frac{3}{2015})+…f(\frac{2013}{2015})+f(\frac{2014}{2015})$=1007.分析 从已知的几个等式发现等式右边是自变量的和,由此得到所求.
解答 解:由已知
$f(\frac{1}{3})+f(\frac{2}{3})=\frac{1}{3}+\frac{2}{3}=1$,
$f(\frac{1}{4})+f(\frac{2}{4})+f(\frac{3}{4})=\frac{1}{4}+\frac{2}{4}+\frac{3}{4}=\frac{3}{2}$,
$f(\frac{1}{5})+f(\frac{2}{5})+f(\frac{3}{5})+f(\frac{4}{5})$=$\frac{1}{5}+\frac{2}{5}+\frac{3}{5}+\frac{4}{5}$=2,
…
$f(\frac{1}{2015})+f(\frac{2}{2015})+f(\frac{3}{2015})+…f(\frac{2013}{2015})+f(\frac{2014}{2015})$=$\frac{1}{2015}+\frac{2}{2015}+\frac{3}{2015}+…+\frac{2014}{2015}$=$\frac{1}{2015}×$$\frac{2014(2014+1)}{2}$=1007.
故答案为:1007
点评 本题考查了归纳推理;关键是由具体的几个等式分析规律,然后猜想一般的规律,再进行计算.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
15.正三角形ABC的边长为2,将它沿高AD翻折,使点B与点C间的距离为$\sqrt{3}$,此时四面体ABCD外接球表面积为( )
| A. | 7π | B. | 19π | C. | $\frac{7}{6}$$\sqrt{7}$π | D. | $\frac{19}{6}$$\sqrt{19}$π |
7.若${∫}_{0}^{1}$(x2+mx)dx=0,则实数m的值为( )
| A. | -$\frac{1}{3}$ | B. | -2 | C. | -1 | D. | -$\frac{2}{3}$ |
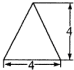 一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.
一个四棱锥的底面是正方形,其正视图和侧视图均为如图所示的等腰三角形,则该四棱锥的侧面积为16$\sqrt{5}$.