题目内容
已知函数f(x)=mx3+nx2(m,n∈R,m>n且m≠0)的图象在(2,f(2))处的切线与x轴平行.(1)试确定m、n的符号;
(2)若函数y=f(x)在区间[n,m]上有最大值为m-n2,试求m的值.
【答案】分析:(1)先对函数f(x)进行求导,又根据f'(2)=0可得到m关于n的代数式.
(2)令f′(x)=3mx2+2nx=3mx2-6mx=0,得x=0或x=2,易证x=0是f(x)的极大值点,x=2是极小值点,
在讨论m的取值范围,根据[n,m]上的最大值,求出m的值.
解答:解:(I)由图象在(2,f(2))处的切线与x轴平行,
知f'(2)=0,∴n=-3m①
又n<m,故n<0,m>0.
(II)令f′(x)=3mx2+2nx=3mx2-6mx=0,
得x=0或x=2
易证x=0是f(x)的极大值点,x=2是极小值点(如图).
令f(x)=f(0)=0,得x=0或x=3.
分类:(I)当0<m≤3时,f(x)max=f(0)=0,∴m-n2=0.②
由①,②解得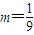 ,符合前提0<m≤3.
,符合前提0<m≤3.
(II)当m>3时,f(x)max=f(m)=m4+m2n,
∴m4+m2n=m-n2.③
由①,③得m3-3m2+9m-1=0.
记g(m)=m3-3m2+9m-1,
∵g′(m)=3m2-6m+9=3(m-1)2+6>0,
∴g(m)在R上是增函数,又m>3,∴g(m)>g(3)=26>0,
∴g(m)=0在(3,+∞)上无实数根.综上,m的值为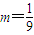 .
.
点评:考查学生利用待定系数法求函数解析式的能力,利用导数研究函数极值和单调性的能力,以及掌握不等式恒成立的条件
(2)令f′(x)=3mx2+2nx=3mx2-6mx=0,得x=0或x=2,易证x=0是f(x)的极大值点,x=2是极小值点,
在讨论m的取值范围,根据[n,m]上的最大值,求出m的值.
解答:解:(I)由图象在(2,f(2))处的切线与x轴平行,
知f'(2)=0,∴n=-3m①
又n<m,故n<0,m>0.
(II)令f′(x)=3mx2+2nx=3mx2-6mx=0,
得x=0或x=2
易证x=0是f(x)的极大值点,x=2是极小值点(如图).
令f(x)=f(0)=0,得x=0或x=3.
分类:(I)当0<m≤3时,f(x)max=f(0)=0,∴m-n2=0.②
由①,②解得
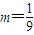 ,符合前提0<m≤3.
,符合前提0<m≤3.(II)当m>3时,f(x)max=f(m)=m4+m2n,
∴m4+m2n=m-n2.③
由①,③得m3-3m2+9m-1=0.
记g(m)=m3-3m2+9m-1,
∵g′(m)=3m2-6m+9=3(m-1)2+6>0,
∴g(m)在R上是增函数,又m>3,∴g(m)>g(3)=26>0,
∴g(m)=0在(3,+∞)上无实数根.综上,m的值为
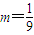 .
.点评:考查学生利用待定系数法求函数解析式的能力,利用导数研究函数极值和单调性的能力,以及掌握不等式恒成立的条件

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目