题目内容
定义:称|b-a|为区间[a,b]的长度,若函数f(x)=
(a<0)的定义域和值域的区间长度相等,则a的值为( )
| ax2+bx+c |
分析:根据函数f(x)=
(a<0)的定义域和值域的区间长度相等,确定函数的定义域与值域,由此可进一步构建方程,从而求得a的值.
| ax2+bx+c |
解答:解:由题意,f(x)的值域为[0,
]
∴函数f(x)=
(a<0)的值域的区间长度为
.
设ax2+bx+c≥0的解集为[x1,x2]
∴|x2-x1|=
∴
=
,又a<0
∴a2=-4a,解得a=-4.
故选A.
|
∴函数f(x)=
| ax2+bx+c |
|
设ax2+bx+c≥0的解集为[x1,x2]
∴|x2-x1|=
|
∴
| ||
| |a| |
|
∴a2=-4a,解得a=-4.
故选A.
点评:本题考查新定义,考查函数的定义域与值域,解题的关键是对新定义的理解,属于基础题.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
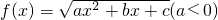 的定义域和值域的区间长度相等,则a的值为
的定义域和值域的区间长度相等,则a的值为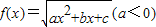 的定义域和值域的区间长度相等,则a的值为( )
的定义域和值域的区间长度相等,则a的值为( )