题目内容
已知任意两个非零向量| a |
| b |
| OA |
| a |
| b |
| OB |
| a |
| b |
| OC |
| a |
| b |
分析:由题意可得向量
与
的坐标,可得
∥
,可得结论.
| AC |
| AB |
| AC |
| AB |
解答:解:∵
=
+
,
=
+2
,
=
+3
,
∴
=
-
=(
+2
)-(
+
)=
,
同理
=
-
=(
+3
)-(
+
)=2
,
∴
=2
,∴
∥
,
∴向量
与
共线,
∴A、B、C三点共线
| OA |
| a |
| b |
| OB |
| a |
| b |
| OC |
| a |
| b |
∴
| AB |
| OB |
| OA |
| a |
| b |
| a |
| b |
| b |
同理
| AC |
| OC |
| OA |
| a |
| b |
| a |
| b |
| b |
∴
| AC |
| AB |
| AC |
| AB |
∴向量
| AC |
| AB |
∴A、B、C三点共线
点评:本题考查向量的共线以及基本运算,属基础题.

练习册系列答案
相关题目


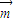 、
、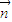 ,向量
,向量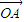 =
=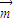 +
+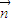 ,
,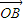 =
=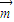 +2
+2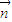 ,
,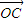 =
=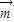 +3
+3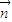 ,则A、B、C三点 构成三角形(填“能”或“不能”)
,则A、B、C三点 构成三角形(填“能”或“不能”)