题目内容
若点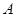 的坐标为
的坐标为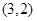 ,
, 是抛物线
是抛物线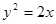 的焦点,点
的焦点,点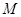 在抛物线上移动时,使
在抛物线上移动时,使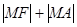 取得最小值的
取得最小值的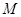 的坐标为( )
的坐标为( )
A.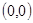 B.
B.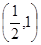 C.
C. D.
D.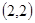
【答案】
D
【解析】
试题分析:由题意得 F( 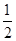 ,0),准线方程为 x=-
,0),准线方程为 x=-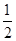 ,设点M到准线的距离为d=|PM|,
,设点M到准线的距离为d=|PM|,
则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,
故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-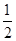 )=
)= 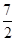 .
.
把 y=2代入抛物线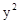 ="2x"
得 x=2,故点M的坐标是(2,2),
="2x"
得 x=2,故点M的坐标是(2,2),
故选D.
考点:本题主要考查抛物线的定义和几何性质。
点评:典型题,解答的关键利用是抛物线定义,体现了转化的数学思想。

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
 ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题. ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.