题目内容
设点F是抛物L:y2=2px(p>0)的焦点,P1,P2,…,Pn是抛物线L上的n个不同的点n(n≥3,n∈N*).(1)当p=2时,试写出抛物线L上三点P1、P2、P3的坐标,时期满足
 ;
;(2)当n≥3时,若
 ,求证:
,求证: ;
;(3)当n>3时,某同学对(2)的逆命题,即:“若
 ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.请你就此从以下三个研究方向中任选一个开展研究:
1.试构造一个说明该命题确实是假命题的反例;
2.对任意给定的大于3的正整数n,试构造该假命题反例的一般形式,并说明你的理由:
3.如果补充一个条件后能使该命题为真,请写出你认为需要补充的一个条件,并说明加上该条件后,能使该逆命题为真命题的理由.
【答案】分析:(1)抛物线l的焦点为F(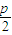 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),利用抛物线的定义可得x1+x2+x3=3,故可取满足条件的三点;
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),利用抛物线的定义可得x1+x2+x3=3,故可取满足条件的三点;
(2)设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn,利用抛物线的定义可得x1+x2+x3+…+xn= ,从而可证
,从而可证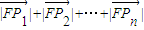 =np
=np
(3)①取n=4时,抛物线l的焦点为F(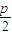 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,利用抛物线的定义,可得x1+x2+x3+x4=2p,从而可得结论;
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,利用抛物线的定义,可得x1+x2+x3+x4=2p,从而可得结论;
②设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn,利用抛物线的定义,可得x1+x2+x3+…+xn=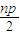 ,从而可得结论;
,从而可得结论;
③补充条件:点Pi的纵坐标满足y1+y2+…+yn=0,即当n>3时,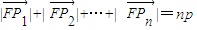 ,点Pi的纵坐标满足y1+y2+…+yn=0,则
,点Pi的纵坐标满足y1+y2+…+yn=0,则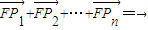 .
.
解答:解:(1)抛物线l的焦点为F(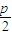 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),
分别过P1、P2、P3作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,
∴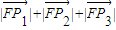 =(x1+
=(x1+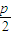 )+(x2+
)+(x2+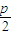 )+(x3+
)+(x3+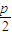 )=x1+x2+x3+
)=x1+x2+x3+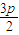 =6
=6
∵p=2,∴x1+x2+x3=3
故可取P1(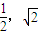 ),P2(1,2),P3(
),P2(1,2),P3( ,
,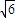 )满足条件;
)满足条件;
(2)设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn
∴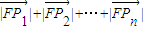 =(x1+
=(x1+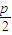 )+(x2+
)+(x2+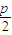 )+(x3+
)+(x3+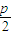 )+…+(xn+
)+…+(xn+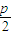 )=x1+x2+x3+…+xn+
)=x1+x2+x3+…+xn+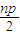
∵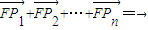
∴x1+x2+x3+…+xn=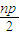
∴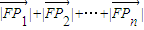 =
=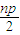 +
+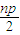 =np
=np
(3)①取n=4时,抛物线l的焦点为F(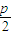 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,
∴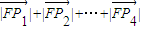 =x1+x2+x3+x4+2p=4p
=x1+x2+x3+x4+2p=4p
∴x1+x2+x3+x4=2p
不妨取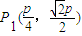 ,
,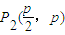 ,
,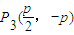 ,
,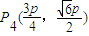 ,则
,则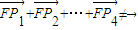
故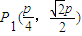 ,
,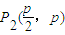 ,
,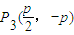 ,
,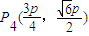 是一个当n=4时,该逆命题的一个反例;
是一个当n=4时,该逆命题的一个反例;
②设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn
∵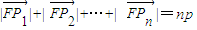 ,∴x1+x2+x3+…+xn+
,∴x1+x2+x3+…+xn+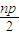 =np,∴x1+x2+x3+…+xn=
=np,∴x1+x2+x3+…+xn=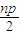
因为上述表达式与点的纵坐标无关,所以将这n点都取在x轴的上方,则它们的纵坐标都大于0,则
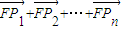 =(0,y1+y2+…+yn)≠
=(0,y1+y2+…+yn)≠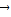
③补充条件:点Pi的纵坐标满足y1+y2+…+yn=0,即当n>3时,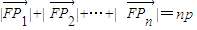 ,点Pi的纵坐标满足y1+y2+…+yn=0,则
,点Pi的纵坐标满足y1+y2+…+yn=0,则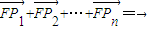
由②知,命题为真.
点评:本题考查抛物线的定义,考查向量的运算,解题的关键是正确运用抛物线的定义,难度较大.
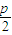 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),利用抛物线的定义可得x1+x2+x3=3,故可取满足条件的三点;
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),利用抛物线的定义可得x1+x2+x3=3,故可取满足条件的三点;(2)设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn,利用抛物线的定义可得x1+x2+x3+…+xn=
 ,从而可证
,从而可证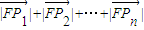 =np
=np(3)①取n=4时,抛物线l的焦点为F(
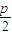 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,利用抛物线的定义,可得x1+x2+x3+x4=2p,从而可得结论;
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,利用抛物线的定义,可得x1+x2+x3+x4=2p,从而可得结论;②设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn,利用抛物线的定义,可得x1+x2+x3+…+xn=
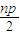 ,从而可得结论;
,从而可得结论;③补充条件:点Pi的纵坐标满足y1+y2+…+yn=0,即当n>3时,
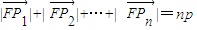 ,点Pi的纵坐标满足y1+y2+…+yn=0,则
,点Pi的纵坐标满足y1+y2+…+yn=0,则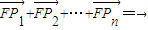 .
.解答:解:(1)抛物线l的焦点为F(
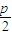 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),分别过P1、P2、P3作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,
∴
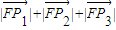 =(x1+
=(x1+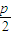 )+(x2+
)+(x2+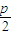 )+(x3+
)+(x3+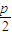 )=x1+x2+x3+
)=x1+x2+x3+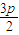 =6
=6∵p=2,∴x1+x2+x3=3
故可取P1(
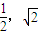 ),P2(1,2),P3(
),P2(1,2),P3( ,
,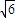 )满足条件;
)满足条件;(2)设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn
∴
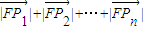 =(x1+
=(x1+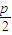 )+(x2+
)+(x2+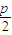 )+(x3+
)+(x3+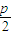 )+…+(xn+
)+…+(xn+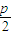 )=x1+x2+x3+…+xn+
)=x1+x2+x3+…+xn+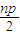
∵
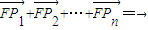
∴x1+x2+x3+…+xn=
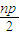
∴
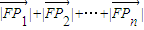 =
=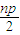 +
+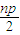 =np
=np(3)①取n=4时,抛物线l的焦点为F(
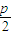 ,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,
,0),设P1(x1,y1),P2(x2,y2),P3(x3,y3),P4(x4,y4),分别过P1、P2、P3,P4作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,Q4,∴
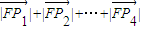 =x1+x2+x3+x4+2p=4p
=x1+x2+x3+x4+2p=4p∴x1+x2+x3+x4=2p
不妨取
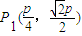 ,
,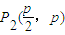 ,
,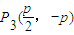 ,
,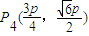 ,则
,则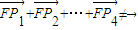
故
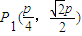 ,
,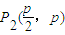 ,
,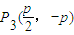 ,
,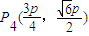 是一个当n=4时,该逆命题的一个反例;
是一个当n=4时,该逆命题的一个反例;②设P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),分别过P1、P2、P3,…,Pn作抛物线的准线l的垂线,垂足分别为Q1、Q2、Q3,…,Qn
∵
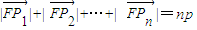 ,∴x1+x2+x3+…+xn+
,∴x1+x2+x3+…+xn+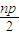 =np,∴x1+x2+x3+…+xn=
=np,∴x1+x2+x3+…+xn=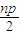
因为上述表达式与点的纵坐标无关,所以将这n点都取在x轴的上方,则它们的纵坐标都大于0,则
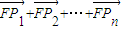 =(0,y1+y2+…+yn)≠
=(0,y1+y2+…+yn)≠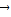
③补充条件:点Pi的纵坐标满足y1+y2+…+yn=0,即当n>3时,
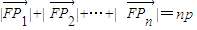 ,点Pi的纵坐标满足y1+y2+…+yn=0,则
,点Pi的纵坐标满足y1+y2+…+yn=0,则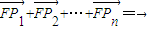
由②知,命题为真.
点评:本题考查抛物线的定义,考查向量的运算,解题的关键是正确运用抛物线的定义,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ;
; ,求证:
,求证: ;
; ,则
,则 ”开展了研究并发现其为假命题.
”开展了研究并发现其为假命题.