题目内容
已知椭圆![]() 是抛物
是抛物
线![]() 的一条切线.
的一条切线.
(I)求椭圆的方程;
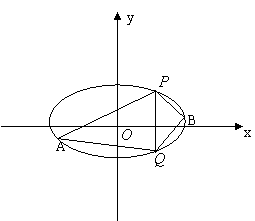
(II)过点![]() 的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
的动直线L交椭圆C于A、B两点,试问:在坐标平面上是否存在一个定点T,使得以AB为直径的圆恒过点T?若存在,求出点T的坐标;若不存在,请说明理由.
解:(I)由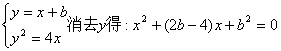
因直线![]() 相切
相切![]()
![]()
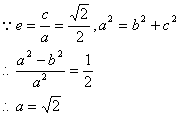
故所求椭圆方程为![]()
(II)当L与x轴平行时,以AB为直径的圆的方程:
![]()
当L与x轴平行时,以AB为直径的圆的方程:![]()
由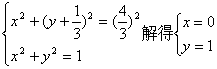
即两圆相切于点(0,1)
因此,所求的点T如果存在,只能是(0,1)
事实上,点T(0,1)就是所求的点,证明如下。
当直线L垂直于x轴时,以AB为直径的圆过点T(0,1)
若直线L不垂直于x轴,可设直线L:![]()
由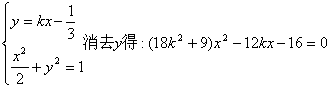
记点![]() 、
、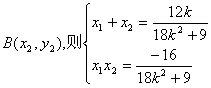
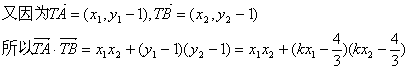
![]()
![]()
所以TA⊥TB,即以AB为直径的圆恒过点T(0,1)
所以在坐标平面上存在一个定点T(0,1)满足条件。

练习册系列答案
相关题目
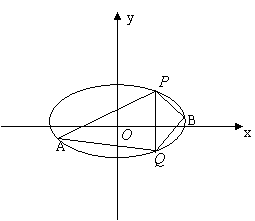 (ii)当
(ii)当