题目内容
已知圆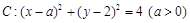 及直线
及直线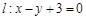 . 当直线
. 当直线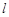 被圆
被圆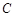 截得的弦长为
截得的弦长为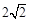 时, 求(1)
时, 求(1)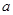 的值; (2)求过点
的值; (2)求过点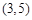 并与圆
并与圆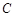 相切的切线方程.
相切的切线方程.
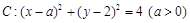 及直线
及直线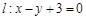 . 当直线
. 当直线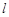 被圆
被圆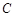 截得的弦长为
截得的弦长为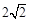 时, 求(1)
时, 求(1)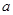 的值; (2)求过点
的值; (2)求过点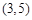 并与圆
并与圆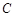 相切的切线方程.
相切的切线方程.(1) ;(2)
;(2) 或
或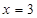
 ;(2)
;(2) 或
或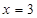
试题分析:(1)涉及直线被圆所截得弦长的计算问题时,一般是利用垂径定理,在以圆心、弦的端点、弦的中点为顶点的直角三角中,利用勾股定理列式求值,该题中先计算圆心到直线
 的距离
的距离 ,可列式为
,可列式为 ,进而求
,进而求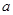 ;(2)先利用点斜式方程设直线为
;(2)先利用点斜式方程设直线为 ,因为直线和圆相切,利用
,因为直线和圆相切,利用 求参数
求参数 ,因为点
,因为点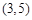 在圆外,所以切线可引两条,则会想到另一条直线必是斜率不存在 情况,再补
在圆外,所以切线可引两条,则会想到另一条直线必是斜率不存在 情况,再补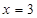 .
.
试题解析:(1)依题意可得圆心
 ,则圆心到直线
,则圆心到直线 的距离
的距离 ,由勾股定理可知
,由勾股定理可知 ,代入化简得
,代入化简得 ,解得
,解得 ,又
,又 ,所以
,所以 ;
;(2)由(1)知圆
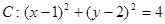 , 又
, 又 在圆外,
在圆外, ①当切线方程的斜率存在时,设方程为
①当切线方程的斜率存在时,设方程为 ,由圆心到切线的距离
,由圆心到切线的距离 可解得
可解得 ,
, 切线方程为
切线方程为 ……9分,②当过
……9分,②当过 斜率不存在,易知直线
斜率不存在,易知直线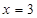 与圆相切,综合①②可知切线方程为
与圆相切,综合①②可知切线方程为 或
或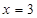 .
.
练习册系列答案
相关题目
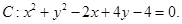 问在圆C上是否存在两点A,B关于直线
问在圆C上是否存在两点A,B关于直线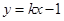 对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程,若不存在,说明理由.
对称,且以AB为直径的圆经过原点?若存在,写出直线AB的方程,若不存在,说明理由. ,
, ,若直线
,若直线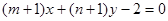 与圆
与圆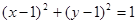 相切,则
相切,则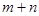 的取值范围是________.
的取值范围是________.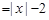 的图像与曲线
的图像与曲线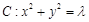 恰好有两个不同的公共点,则实数
恰好有两个不同的公共点,则实数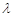 的取值范围为 .
的取值范围为 . 的切线方程中有一个是( )
的切线方程中有一个是( )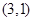 作圆
作圆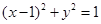 的两条切线,切点分别为
的两条切线,切点分别为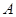 ,
,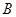 ,则直线
,则直线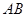 的方程为( )
的方程为( )



 截圆
截圆 得到的弦长为( )
得到的弦长为( )

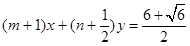 与圆
与圆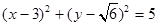 相切,若对任意的
相切,若对任意的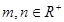 均有不等式
均有不等式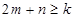 成立,那么正整数
成立,那么正整数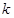 的最大值是( )
的最大值是( ) ,则直线
,则直线 被圆
被圆 所截得的弦长为 ( )
所截得的弦长为 ( ) 

