题目内容
已知直线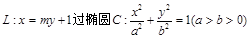 的右焦点F,且交椭圆C于A,B两点.
的右焦点F,且交椭圆C于A,B两点.
(1)若抛物线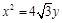 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;
(2)对椭圆C,若直线L交y轴于点M,且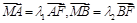 ,当m变化时,求
,当m变化时,求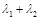 的值.
的值.
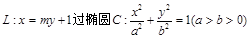 的右焦点F,且交椭圆C于A,B两点.
的右焦点F,且交椭圆C于A,B两点.(1)若抛物线
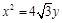 的焦点为椭圆C的上顶点,求椭圆C的方程;
的焦点为椭圆C的上顶点,求椭圆C的方程;(2)对椭圆C,若直线L交y轴于点M,且
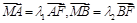 ,当m变化时,求
,当m变化时,求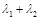 的值.
的值.解:(1)易知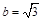 ,
,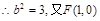 ,
,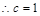 ,
,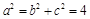 .
.  .
.
(2)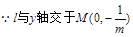 ,设
,设 ,则由
,则由 可得:
可得:
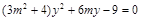 ,故
,故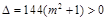 .
. 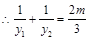 .
.
又由 得
得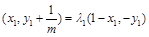 .
.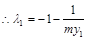 . 同理
. 同理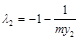 .
.
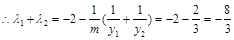 .
.
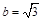 ,
,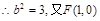 ,
,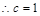 ,
,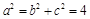 .
.  .
.(2)
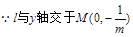 ,设
,设 ,则由
,则由 可得:
可得: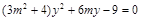 ,故
,故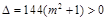 .
. 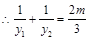 .
.又由
 得
得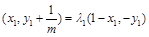 .
.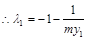 . 同理
. 同理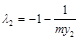 .
.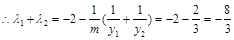 .
.本试题主要考查同学们能利用圆锥曲线的性质求解椭圆的标准方程,以及利用直线与椭圆的位置关系联立方程组,结合韦达定理,表示向量的坐标,进而消去参数求解定值数学思想。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
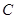 的极坐标方程是
的极坐标方程是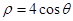 . 以极点为平面直角坐标系的原点,极轴为
. 以极点为平面直角坐标系的原点,极轴为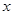 轴的正半轴,建立平面直角坐标系,直线
轴的正半轴,建立平面直角坐标系,直线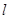 的参数方程是:
的参数方程是: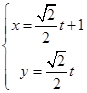 (
(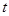 为参数),则直线
为参数),则直线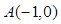 ,
,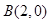 ,动点满足条件
,动点满足条件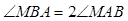 ,动点
,动点 的轨迹方程是 .
的轨迹方程是 .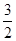 ),动圆P经过点F且和直线y=
),动圆P经过点F且和直线y=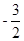 相切,记动圆的圆心P的轨迹为曲线W.
相切,记动圆的圆心P的轨迹为曲线W. ,
, ,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。
,分别交曲线W于A,B和C,D.①求四边形ABCD面积的最小值;②分别在A,B两点作曲线W的切线,这两条切线的交点记为Q,求证:QA⊥QB,且点Q在某一定直线上。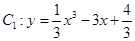 ,曲线
,曲线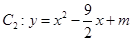 ,若当
,若当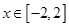 时,曲线
时,曲线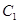 在曲线
在曲线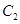 的下方,则实数
的下方,则实数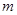 的取值范围是 .
的取值范围是 . :
: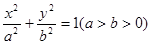 的右焦点
的右焦点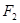 引直线
引直线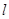 ,与
,与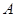 点,与
点,与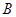 、
、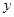 轴交于
轴交于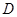 点,若
点,若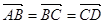 ,则
,则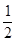
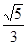
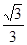
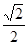 .
.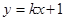 与曲线
与曲线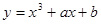 切于点
切于点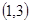 ,则
,则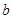 的值为( )
的值为( )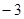
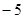
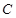 :
: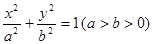 的离心率为
的离心率为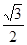 ,过坐标原点
,过坐标原点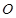 且斜率为
且斜率为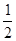 的直线
的直线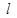 与
与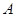 、
、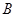 ,
,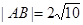 .
.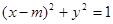 与椭圆
与椭圆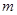 的取值范围.
的取值范围.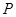 在曲线
在曲线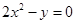 上移动,则点
上移动,则点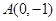 与点
与点