题目内容
P(a,b)是平面上的一个点,设事件A表示“|a-b|<2”,
其中a,b为实常数.
(1)若a,b均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若a,b均为从区间[0,5)任取的一个数,求事件A发生的概率.
其中a,b为实常数.
(1)若a,b均为从0,1,2,3,4五个数中任取的一个数,求事件A发生的概率;
(2)若a,b均为从区间[0,5)任取的一个数,求事件A发生的概率.
分析:(1)先确定a、b取值的所有情况得到共有多少种情况,又因为|a-b|<2,所以事件“|a-b|<2”的情况数,所以即可求得事件“|a-b|<2”的概率;
(2)本小题是一个几何概型的概率问题,先根据闭区间[0,5]上等可能地随机取两个数a,b及点P落在区域|a-b|<2内,得到试验发生包含的事件对应的区域和满足条件的事件对应的区域,做出面积,利用几何概型计算公式得到结果.
(2)本小题是一个几何概型的概率问题,先根据闭区间[0,5]上等可能地随机取两个数a,b及点P落在区域|a-b|<2内,得到试验发生包含的事件对应的区域和满足条件的事件对应的区域,做出面积,利用几何概型计算公式得到结果.
解答: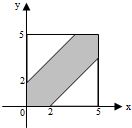 解(1)这是一个古典概型,事件A的基本事件为(0,0),(0,1),(1,0),(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4).
解(1)这是一个古典概型,事件A的基本事件为(0,0),(0,1),(1,0),(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4).
而基本事件的总数为5×5=25,所以事件A发生的概率是
.----------(5分)
(2)如图,试验的全部结果所构成的区域为一个正方形区域,面积为SΩ=25,
事件A所构成的区域为A={a,b)|0≤a<5,0≤b<5,-2<a-b<2},即图中的阴影部分,面积为SA=16,这是一个几何概型,所以P(A)=SA/SΩ=
.------------(10分)
 解(1)这是一个古典概型,事件A的基本事件为(0,0),(0,1),(1,0),(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4).
解(1)这是一个古典概型,事件A的基本事件为(0,0),(0,1),(1,0),(1,1),(1,2),(2,1),(2,2),(2,3),(3,2),(3,3),(3,4),(4,3),(4,4).而基本事件的总数为5×5=25,所以事件A发生的概率是
| 13 |
| 25 |
(2)如图,试验的全部结果所构成的区域为一个正方形区域,面积为SΩ=25,
事件A所构成的区域为A={a,b)|0≤a<5,0≤b<5,-2<a-b<2},即图中的阴影部分,面积为SA=16,这是一个几何概型,所以P(A)=SA/SΩ=
| 16 |
| 25 |
点评:古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积、和体积的比值得到.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.