��Ŀ����
�踴����=x+yi��x��y��R���븴ƽ���ϵ�P��x��y����Ӧ����1�������ǹ���t��һԪ���η���t2-2t+m=0��m��R����һ���������|��|=2����ʵ��m��ֵ��
��2���踴������������|��+3|+��-1��n|��-3|=3a+��-1��na������n��N*������a�� (
| 3 |
| 2 |
| 2 |
��3���ڣ�2���������£��켣C2�ϴ��ڵ�A��ʹ��A���B��x0��0����x0��0������С���벻С��
2
| ||
| 3 |
��������1����ʵϵ����������ɶԣ�����Τ�ﶨ��ֱ�����m��ֵ��
��2������һ����nΪ������ż��������a�ķ�Χ������˫���߷��̣����aֵ���Ƴ�˫���߷��̼��ɣ�
���������������a����ż�������������飬��������£����a������˫���ߵĶ������˫���߷��̣�
��3�����A�����꣬���|AB|����ʽ������x��Χ��x�ĶԳ�������0��x0��
��x0��
ʱ��|AB|����Сֵ����С��
�����ʵ��x0��ȡֵ��Χ��
��2������һ����nΪ������ż��������a�ķ�Χ������˫���߷��̣����aֵ���Ƴ�˫���߷��̼��ɣ�
���������������a����ż�������������飬��������£����a������˫���ߵĶ������˫���߷��̣�
��3�����A�����꣬���|AB|����ʽ������x��Χ��x�ĶԳ�������0��x0��
3
| ||
| 2 |
3
| ||
| 2 |
2
| ||
| 3 |
����⣺��1�����Ƿ��̵�һ���������
�Ƿ��̵���һ���������2�֣�
����•
=m=|��|2=4������m=4��2�֣�
��2������1���ٵ�nΪ����ʱ��|��+3|-|��-3|=2a������a�� (
�� 3)����
�켣C1Ϊ˫���ߣ��䷽��Ϊ
-
=1����2�֣�
�ڵ�nΪż��ʱ��|��+3|+|��-3|=4a������a�� (
�� 3)����
�켣C2Ϊ��Բ���䷽��Ϊ
+
=1����2�֣�
������÷�����
?
���a2=3��
��Ϊ
��a��3������a=
��
��ʱ�켣ΪC1��C2�ķ��̷ֱ��ǣ�
-
=1��
+
=1����2�֣�
����2���������
?
��2�֣�
�켣ΪC1��C2��������D(2��
)���ҵ�D(2��
)��Ӧ�ĸ�����=2+
i��
������ʽ��a=
����2�֣�
��|��+3|-|��-3|=2
��Ӧ�Ĺ켣C1��˫���ߣ�����Ϊ
-
=1��
|��+3|+|��-3|=4
��Ӧ�Ĺ켣C2����Բ������Ϊ
+
=1����2�֣�
��3���ɣ�2��֪���켣C2��
+
=1�����A��������x��y����
��|AB|2=(x-x0)2+y2=(x-x0)2+3-
x2
=
x2-2x0x+
+3=
(x-
x0)2+3-
��
x��[-2
��2
]��2�֣�
��0��
x0��2
��0��x0��
ʱ��|AB|2min=3-
��
?0��x0��
��
x0��2
��x0��
ʱ��|AB|min=|x0-2
|��
?x0��
����2�֣�
����0��x0��
��x0��
����2�֣���
. |
| �� |
����•
. |
| �� |
��2������1���ٵ�nΪ����ʱ��|��+3|-|��-3|=2a������a�� (
| 3 |
| 2 |
�켣C1Ϊ˫���ߣ��䷽��Ϊ
| x2 |
| a2 |
| y2 |
| 9-a2 |
�ڵ�nΪż��ʱ��|��+3|+|��-3|=4a������a�� (
| 3 |
| 2 |
�켣C2Ϊ��Բ���䷽��Ϊ
| x2 |
| 4a2 |
| y2 |
| 4a2-9 |
������÷�����
|
|
���a2=3��
��Ϊ
| 3 |
| 2 |
| 3 |
��ʱ�켣ΪC1��C2�ķ��̷ֱ��ǣ�
| x2 |
| 3 |
| y2 |
| 6 |
| x2 |
| 12 |
| y2 |
| 3 |
����2���������
|
|
�켣ΪC1��C2��������D(2��
| 2 |
| 2 |
| 2 |
������ʽ��a=
| 3 |
��|��+3|-|��-3|=2
| 3 |
| x2 |
| 3 |
| y2 |
| 6 |
|��+3|+|��-3|=4
| 3 |
| x2 |
| 12 |
| y2 |
| 3 |
��3���ɣ�2��֪���켣C2��
| x2 |
| 12 |
| y2 |
| 3 |
��|AB|2=(x-x0)2+y2=(x-x0)2+3-
| 1 |
| 4 |
=
| 3 |
| 4 |
| x | 2 0 |
| 3 |
| 4 |
| 4 |
| 3 |
| 1 |
| 3 |
| x | 2 0 |
x��[-2
| 3 |
| 3 |
��0��
| 4 |
| 3 |
| 3 |
3
| ||
| 2 |
| 1 |
| 3 |
| x | 2 0 |
| 4 |
| 3 |
| 5 |
��
| 4 |
| 3 |
| 3 |
3
| ||
| 2 |
| 3 |
2
| ||
| 3 |
8
| ||
| 3 |
����0��x0��
| 5 |
8
| ||
| 3 |
���������⿼�鸴���Ļ�������켣���̣�ֱ����Բ���ߵ��ۺ����⣬�����������˼�룬ת��˼�룬���е��⣮

��ϰ��ϵ�д�
�����Ŀ
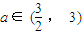 ������nΪ����ʱ������P��x��y���Ĺ켣ΪC1����nΪż��ʱ������P��x��y���Ĺ켣ΪC2�����������߶�������
������nΪ����ʱ������P��x��y���Ĺ켣ΪC1����nΪż��ʱ������P��x��y���Ĺ켣ΪC2�����������߶�������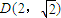 ����켣C1��C2�ķ��̣�
����켣C1��C2�ķ��̣�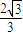 ����ʵ��x��ȡֵ��Χ��
����ʵ��x��ȡֵ��Χ��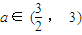 ������nΪ����ʱ������P��x��y���Ĺ켣ΪC1����nΪż��ʱ������P��x��y���Ĺ켣ΪC2�����������߶�������
������nΪ����ʱ������P��x��y���Ĺ켣ΪC1����nΪż��ʱ������P��x��y���Ĺ켣ΪC2�����������߶�������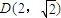 ����켣C1��C2�ķ��̣�
����켣C1��C2�ķ��̣�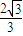 ����ʵ��x��ȡֵ��Χ��
����ʵ��x��ȡֵ��Χ��