题目内容
10.若a2+b2=4c2(c≠0),则直线ax+by+2c=0被圆x2+y2=2所截得的弦长为2.分析 求出圆心到直线的距离,利用弦心距、半径、半弦长满足勾股定理,求出半弦长,即可求出结果.
解答 解:圆的圆心(0,0)到直线ax+by+2c=0的距离为:$\frac{|2c|}{\sqrt{{a}^{2}+{b}^{2}}}$=1,
因为圆的半径为$\sqrt{2}$,
所以直线ax+by+2c=0被圆x2+y2=2所截得的弦长为:2$\sqrt{2-1}$=2.
故答案为:2.
点评 本题是基础题,考查直线被圆截得的弦长的求法,注意点到直线的距离公式的应用,弦心距、半径、半弦长满足勾股定理,是快速解题的关键.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
20.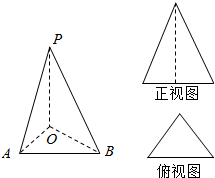 若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
 若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )
若三棱锥P-ABC的正视图为如图所示边长为2的正三角形,俯视图为等腰直角三角形,则三棱锥的体积是( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
18.三个数0.993.3,log3π,log20.8的大小关系为( )
| A. | log20.8<0.993.3<log3π | B. | log20.8<log3π<0.993.3 | ||
| C. | 0.993.3<log20.81<log3π | D. | log3π<0.993.3<log20.8 |
5.已知点A(2,3),B(-3,-2),若直线l过点P(1,1)与线段AB相交,则直线l的斜率k的取值范围是( )
| A. | k≥2或k≤$\frac{3}{4}$ | B. | $\frac{3}{4}$≤k≤2 | C. | k≥$\frac{3}{4}$ | D. | k≤2 |
2.下列函数中,在区间(0,+∞)上增长速度越来越快的是( )
| A. | y=20071nx | B. | y=x2007 | C. | y=$\frac{{e}^{x}}{2007}$ | D. | y=2007•2x |
19.已知函数f(x)=$\left\{\begin{array}{l}{(2a-1)x+3a,x≤1}\\{lo{g}_{a}x,x>1}\end{array}\right.$满足对任意的实数x1≠x2,都有$\frac{f({x}_{2})-f({x}_{1})}{{x}_{1}-{x}_{2}}$>0成立,则实数a的取值范围是( )
| A. | (0,1) | B. | (0,$\frac{1}{2}$) | C. | [$\frac{1}{5}$,$\frac{1}{2}$) | D. | [$\frac{1}{5}$,1) |