题目内容
函数f(x)是定义域为R的奇函数,且当x≥0时,f(x)=2x-x+α,则函数f(x)的零点个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:根的存在性及根的个数判断,函数奇偶性的性质
专题:函数的性质及应用
分析:根据奇偶性得出α=-1,当x≥0时,f(x)=2x-x-1,设x<0,则-x>0,f(x)=-f(-x)=-(2-x+x-1)=-2-x-x+1,运用图象判断即可.
解答:
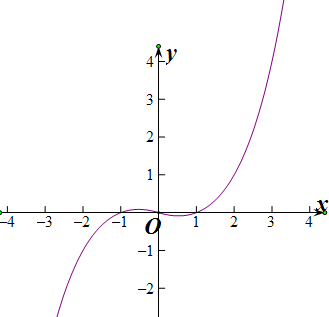 解:∵函数f(x)是定义域为R的奇函数,
解:∵函数f(x)是定义域为R的奇函数,
∴当x≥0时,f(x)=2x-x+α,
∴f(0)=0
1-0+α=0,
α=-1,
∴当x≥0时,f(x)=2x-x-1,
设x<0,则-x>0,
f(x)=-f(-x)=-(2-x+x-1)=-2-x-x+1,
据图判断函数f(x)的零点个数是3个,
故选:C
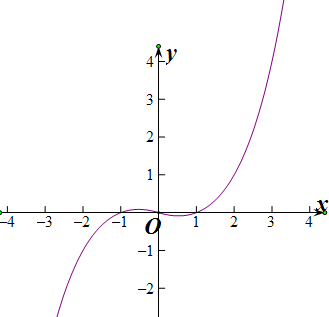 解:∵函数f(x)是定义域为R的奇函数,
解:∵函数f(x)是定义域为R的奇函数,∴当x≥0时,f(x)=2x-x+α,
∴f(0)=0
1-0+α=0,
α=-1,
∴当x≥0时,f(x)=2x-x-1,
设x<0,则-x>0,
f(x)=-f(-x)=-(2-x+x-1)=-2-x-x+1,
据图判断函数f(x)的零点个数是3个,
故选:C
点评:本题考查了函数的奇偶性,解析式的求解,数形结合的思想,属于中档题.

练习册系列答案
相关题目
若|
|=2,|
|=1,
和
夹角为60°,则|
+2
|=( )
| a |
| b |
| a |
| b |
| a |
| b |
| A、2 | ||
| B、4 | ||
| C、3 | ||
D、2
|
已知命题p:a<0时方程ax2+2x+1=0至少有一个负数根( )
| A、¬p是真命题 |
| B、p的逆命题是真命题 |
| C、p的否命题是真命题 |
| D、p的逆否命题是真命题 |
若曲线 y=x2 上P点处的切线平行于 2x-y+1=0,则点P的坐标是( )
| A、( 1,-1) |
| B、(-1,1) |
| C、( 1,1) |
| D、(-1,-1) |