题目内容
在关于人体脂肪含量 (百分比)和年龄
(百分比)和年龄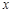 关系的研究中,得到如下一组数据
关系的研究中,得到如下一组数据
年龄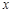 | 23 | 27 | 39 | 41 | 45 | 50 |
脂肪含量 | 9.5 | 17.8 | 21.2 | 25.9 | 27.5 | 28.2 |
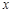 与
与 是否具有相关关系;
是否具有相关关系;
(Ⅱ)通过计算可知
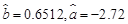 ,
,请写出
 对
对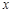 的回归直线方程,并计算出
的回归直线方程,并计算出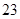 岁和
岁和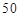 岁的残差.
岁的残差.
(Ⅰ)从图中可看出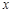 与
与 具有相关关系.
具有相关关系.
(Ⅱ)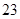 岁和
岁和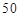 岁的残差分别为
岁的残差分别为 和
和 .
.
解析试题分析:(Ⅰ)涉及两个变量,年龄与脂肪含量.
因此选取年龄为自变量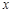 ,脂肪含量为因变量
,脂肪含量为因变量 .
.
作散点图,从图中可看出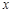 与
与 具有相关关系.
具有相关关系.
┄┄┄┄┄┄┄┄┄┄┄┄5分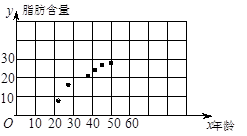
(Ⅱ) 对
对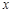 的回归直线方程为
的回归直线方程为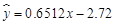 .
.
当 时,
时,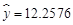 ,
, .
.
当 时,
时,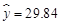 ,
, .
.
所以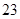 岁和
岁和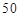 岁的残差分别为
岁的残差分别为 和
和 . 10分
. 10分
考点:本题主要考查散点图,相关性,线性回归直线方程,残差的概念。
点评:中档题,正相关,两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由大到小或由小到大变化。负相关,两个变量变动方向相同,一个变量由大到小或由小到大变化时,另一个变量亦由小到大或由大到小变化。从散点图看,就是自左向右升(降)。

练习册系列答案
相关题目
为了研究玉米品种对产量的影响,某农科院对一块试验田种植的一批玉米共10000 株的生长情况进行研究,现采用分层抽样方法抽取50株作为样本,统计结果如下:
| | 高茎 | 矮茎 | 合计 |
| 圆粒 | 11 | 19 | 30 |
| 皱粒 | 13 | 7 | 20 |
| 合计 | 24 | 26 | 50 |
(2) 根据对玉米生长情况作出的统计,是否能在犯错误的概率不超过0.050的前提下认为玉米的圆粒与玉米的高茎有关?(下面的临界值表和公式可供参考:
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
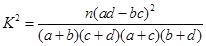 ,其中
,其中 )
) 某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 | 10 | | |
| 乙班 | | 30 | |
| 合计 | | | 110 |
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.附:
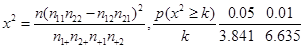
在研究色盲与性别的关系调查中,调查了男性480人,其中有38人患色盲,调查的520名女性中有6人患色盲.
(1)根据以上数据建立一个2×2列联表;
| | 患色盲 | 不患色盲 | 总计 |
| 男 | | 442 | |
| 女 | 6 | | |
| 总计 | 44 | 956 | 1000 |
随机变量

附临界值参考表:
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
某种产品的广告费用支出 (百万)与销售额
(百万)与销售额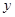 (百万)之间有如下的对应数据:
(百万)之间有如下的对应数据:
 | 2 | 4 | 5 | 6 | 8 |
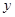 | 30 | 40 | 60 | 50 | 70 |
(2)求回归直线方程;
(3)据此估计广告费用为10(百万)时,销售收入
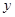 的值.
的值. 为了调查胃病是否与生活规律有关,调查某地540名40岁以上的人得结果如下:
| | 患胃病 | 未患胃病 | 合计 |
| 生活不规律 | 60 | 260 | 320 |
| 生活有规律 | 20 | 200 | 220 |
| 合计 | 80 | 460 | 540 |
(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
| 月份 | 用气量(立方米) | 煤气费(元) |
| 1 | 4 | 4.00 |
| 2 | 25 | 14.00 |
| 3 | 35 | 19.00 |
该市煤气收费的方法是:煤气费=基本费十超额费十保险费.
若每月用气量不超过最低额度
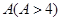 立方米时,只付基本费
立方米时,只付基本费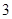 元和每户每月定额保险费
元和每户每月定额保险费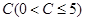 元;若用气量超过
元;若用气量超过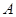 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付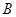 元.
元.(1)根据上面的表格求
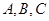 的值;
的值;(2)记用户第四月份用气为
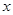 立方米,求他应交的煤气费
立方米,求他应交的煤气费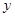 (元).
(元). 

 2列联表进行独立性检验,经计算K2=4.069,参考下表你能得到什么统计学结论?
2列联表进行独立性检验,经计算K2=4.069,参考下表你能得到什么统计学结论?  ≥k0)
≥k0)