题目内容
给出下列关于互不相同的直线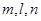 和平面
和平面 的四个命题:
的四个命题:
①若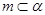 ,
,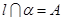 ,点
,点 ,则
,则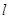 与
与 不共面;
不共面;
②若 、
、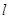 是异面直线,
是异面直线,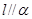 ,
,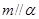 ,且
,且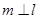 ,
,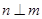 ,则
,则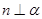 ;
;
③若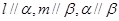 ,则
,则 ;
;
④若 ,
,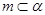 ,
,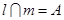 ,
,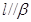 ,
, ,则
,则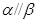 .
.
其中为假命题的是( )
A.① B.② C.④ D.③
【答案】
D
【解析】
试题分析:对于命题①,假设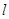 与
与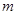 共面,则直线
共面,则直线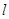 与
与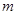 平行或相交,由于
平行或相交,由于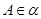 ,
,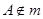 ,则点
,则点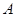 和直线
和直线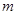 确定平面
确定平面 ,又直线
,又直线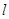 与
与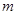 共面,则直线
共面,则直线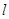 与
与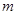 确定平面
确定平面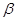 ,则直线
,则直线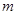 为平面
为平面 与平面
与平面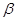 的交线,由于
的交线,由于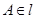 而
而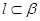 ,所以
,所以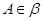 ,由公理
,由公理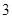 可知,
可知,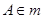 ,这与
,这与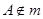 矛盾,故假设不成立,故
矛盾,故假设不成立,故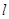 与
与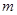 不共面,命题①为真命题;对于命题②,因为
不共面,命题①为真命题;对于命题②,因为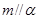 ,则在平面
,则在平面 存在直线
存在直线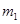 ,使得
,使得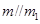 ,同理,在平面内存在直线
,同理,在平面内存在直线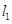 ,使得
,使得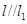 ,由于直线
,由于直线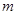 与直线
与直线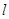 为异面直线,则
为异面直线,则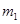 与
与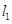 相交,
相交,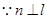 且
且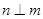 ,所以
,所以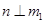 且
且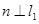 ,由于
,由于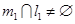 ,所以
,所以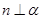 ;对于命题③,如
;对于命题③,如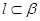 ,
,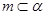 ,当
,当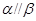 时,
时,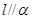 ,
,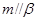 ,但是直线
,但是直线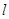 与
与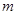 无交点,则直线
无交点,则直线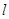 与
与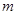 平行或异面,故命题③错误;对于命题④,由平面与平面平行的判定定理可知命题④正确,故选D.
平行或异面,故命题③错误;对于命题④,由平面与平面平行的判定定理可知命题④正确,故选D.
考点:空间中点、线、面的位置关系

练习册系列答案
相关题目