题目内容
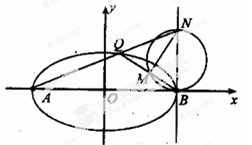
设椭圆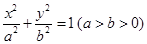 的左右顶点分别为
的左右顶点分别为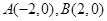 ,离心率
,离心率 .过该椭圆上任一点
.过该椭圆上任一点 作
作 轴,垂足为
轴,垂足为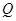 ,点
,点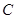 在
在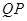 的延长线上,且
的延长线上,且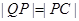 .
.
(1)求椭圆的方程;
(2)求动点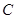 的轨迹
的轨迹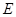 的方程;
的方程;
(3)设直线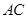 (
(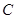 点不同于
点不同于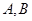 )与直线
)与直线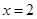 交于点
交于点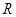 ,
,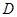 为线段
为线段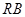 的中点,试判断直线
的中点,试判断直线 与曲线
与曲线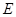 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(1)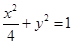 ;(2)
;(2)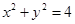 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)根据椭圆的几何性质求出椭圆标准方程中的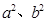 ;(2)用设点、建立两个动点之间坐标的关系和代入已知曲线方程的方法求出动点轨迹方程;(3)先利用
;(2)用设点、建立两个动点之间坐标的关系和代入已知曲线方程的方法求出动点轨迹方程;(3)先利用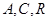 三点共线建立
三点共线建立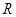 与
与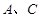 的坐标关系,再根据
的坐标关系,再根据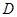 为线段
为线段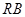 的中点求出
的中点求出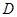 的坐标表达式,进一步求出直线
的坐标表达式,进一步求出直线 的方程,最后根据曲线
的方程,最后根据曲线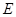 圆心到直线
圆心到直线 的距离与半径的大小情况判断其位置关系.
的距离与半径的大小情况判断其位置关系.
试题解析:(1)由题意可得 ,
,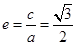 ,∴
,∴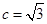 , 2分
, 2分
∴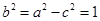 ,所以椭圆的方程为
,所以椭圆的方程为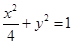 . 4分
. 4分
(2)设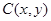 ,
,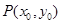 ,由题意得
,由题意得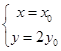 ,即
,即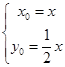 , 6分
, 6分
又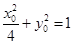 ,代入得
,代入得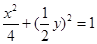 ,即
,即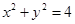 .
.
即动点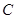 的轨迹
的轨迹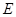 的方程为
的方程为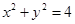 . 8分
. 8分
(3)设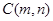 ,点
,点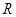 的坐标为
的坐标为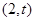 ,∵
,∵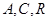 三点共线,∴
三点共线,∴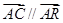 ,
,
而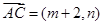 ,
,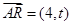 ,则
,则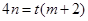 ,∴
,∴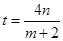 ,
,
∴点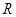 的坐标为
的坐标为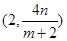 ,点
,点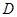 的坐标为
的坐标为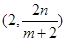 , 10分
, 10分
∴直线 的斜率为
的斜率为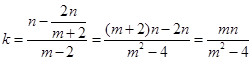 ,
,
而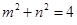 ,∴
,∴ ,∴
,∴ , 12分
, 12分
∴直线 的方程为
的方程为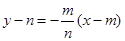 ,化简得
,化简得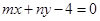 ,
,
∴圆心 到直线
到直线 的距离
的距离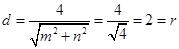 ,
,
所以直线 与圆
与圆 相切. 14分
相切. 14分
考点:1、椭圆的标准方程,2、代入法求动点轨迹方程,3、直线与圆位置关系的判定问题.

练习册系列答案
相关题目
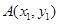 ,
,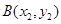 是抛物线
是抛物线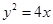 上相异两点,且满足
上相异两点,且满足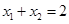 .
.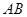 的中垂线经过点
的中垂线经过点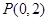 ,求直线
,求直线 轴于点
轴于点 ,求
,求 的面积的最大值及此时直线
的面积的最大值及此时直线 .
.
 的参数方程为
的参数方程为 (t为参数,0<a<
(t为参数,0<a< ),曲线C的极坐标方程为
),曲线C的极坐标方程为 .
.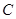 :
: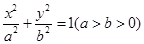 的离心率为
的离心率为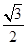 ,以椭圆
,以椭圆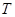 为圆心作圆
为圆心作圆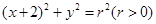 ,设圆
,设圆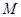 与点
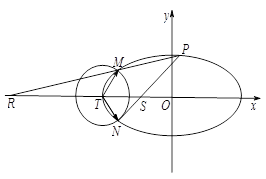
与点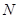 .
.
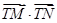 的最小值,并求此时圆
的最小值,并求此时圆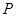 是椭圆
是椭圆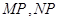 分别与
分别与 轴交于点
轴交于点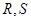 ,
, 为坐标原点,
为坐标原点,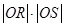 为定值.
为定值.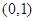 ,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.
,且在x轴上截得弦长为2,记该圆圆心的轨迹为E.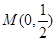 的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为
的直线m交曲线E于A,B两点,过A,B两点分别作曲线E的切线,两切线交于点C,当△ABC的面积为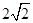 时,求直线m的方程.
时,求直线m的方程.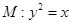 与曲线
与曲线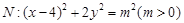 相交于
相交于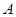 、
、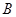 、
、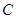 、
、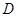 四个点.
四个点.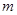 的取值范围;
的取值范围;  的面积的最大值及此时对角线
的面积的最大值及此时对角线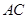 与
与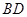 的交点坐标.
的交点坐标.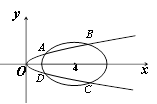
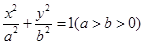 的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.
的左、右焦点分别为F1(-1,0),F2(1,0),过F1作与x轴不重合的直线l交椭圆于A,B两点.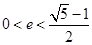 ,
,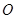 为坐标原点,求证:
为坐标原点,求证: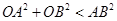 .
.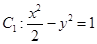 ,曲线
,曲线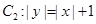 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.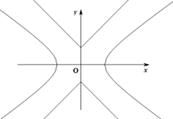
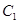 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);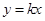 与
与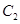 有公共点,求证
有公共点,求证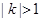 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;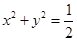 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.