题目内容
【题目】如图,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.
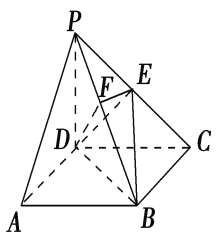
(1)求证:PA∥平面EDB;
(2)求证:PB⊥平面EFD;
(3)求二面角C-PB-D的大小.
【答案】(1)详见解析(2)详见解析(3) 60°
【解析】
试题分析:(1)连接AC,AC交BD于O,连接EO要证明PA∥平面EDB,只需证明直线PA平行平面EDB内的直线EO;(2)要证明PB⊥平面EFD,只需证明PB垂直平面EFD内的两条相交直线DE、EF,即可;(3)必须说明∠EFD是二面角C-PB-D的平面角,然后求二面角C-PB-D的大小
试题解析:(1)证明: 如图所示,连接AC,AC交BD于O,连接EO.
∵底面ABCD是正方形,
∴点O是AC的中点.
在△PAC中,EO是中位线,
∴PA∥EO. ……2
而EO平面EDB且PA平面EDB,
∴PA∥平面EDB. ……4
(2)证明: ∵PD⊥底面ABCD,且DC底面ABCD,
∴PD⊥DC.
∵PD=DC,可知△PDC是等腰直角三角形.
而DE是斜边PC的中线,∴DE⊥PC.① ……6
同样,由PD⊥底面ABCD,BC平面ABCD,得PD⊥BC.
∵底面ABCD是正方形,有DC⊥BC,又PD∩CD=D,
∴BC⊥平面PDC.
而DE平面PDC,∴BC⊥DE.②
由①和②且PC∩BC=C可得DE⊥平面PBC.
而PB平面PBC,∴DE⊥PB.
又EF⊥PB且DE∩EF=E,
∴PB⊥平面EFD. ……8
(3)解 由(2)知,PB⊥DF.
故∠EFD是二面角C-PB-D的平面角. ……9
由(2)知DE⊥EF,PD⊥DB.
设正方形ABCD的边长为a,
则PD=DC=a,BD=![]() a,
a,
PB=![]() a,PC=
a,PC=![]() a,DE=
a,DE=![]() a,
a,
在Rt△PDB中,DF=![]() a.
a.
在Rt△EFD中,sin∠EFD=![]() ,
,
∴∠EFD=60°. ……11
∴二面角C-PB-D的大小为60°. ……12

【题目】某单位每天的用电量![]() (度)与当天最高气温
(度)与当天最高气温![]() (℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
(℃)之间具有线性相关关系,下表是该单位随机统计4天的用电量与当天最高气温的数据.
最高气温(℃) | 26 | 29 | 31 | 34 |
用电量 (度) | 22 | 26 | 34 | 38 |
(Ⅰ)根据表中数据,求出回归直线的方程![]() (其中
(其中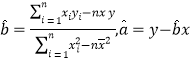 );
);
(Ⅱ)试预测某天最高气温为33℃时,该单位当天的用电量(精确到1度).