题目内容
设二次函数f(x)=ax2+bx+c(a,b,c∈R)满足下列条件:①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)恒成立;②当x∈(0,5)时,x≤f(x)≤2|x-1|+1恒成立.
(1)求f(1)的值;
(2)求f(x)的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当x∈[1,m]时,就有f(x+t)≤x成立.
答案:
解析:
解析:
|
解:(1)在②中令 (2)由①知二次函数关于直线 (3)因为 令 当 当 |

练习册系列答案
相关题目
 R,且x+y+z=1,求证x2+y2+z2≥
R,且x+y+z=1,求证x2+y2+z2≥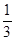 ;
; ,若x
,若x