题目内容
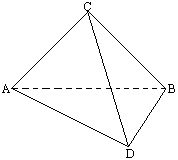
如图所示,平面ABCD⊥平面ABEF,ABCD是正方形,ABEF是矩形,且AF=![]() AD=
AD=![]() ,G为EF的中点,
,G为EF的中点,
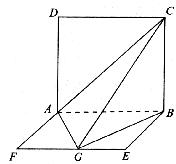
(1)求证:平面AGC⊥平面BGC;
(2)求GB与平面AGC所成角的正弦值;
(3)求二面角B―AC―G的大小.
解:(1)正方形ABCD![]() CB⊥AB.∵面ABCD⊥面ABEF,且交于AB.∴CB⊥面ABEF.
CB⊥AB.∵面ABCD⊥面ABEF,且交于AB.∴CB⊥面ABEF.
∵AG、GB![]() 面ABEF,∴CB⊥AG,CB⊥BG.
面ABEF,∴CB⊥AG,CB⊥BG.
又AD=2![]() ,AF=
,AF=![]() ,四边形ABEF是矩形,G是EF的中点,
,四边形ABEF是矩形,G是EF的中点,
∴AG=BG=![]() ,AB=2
,AB=2![]() ,AB2=AG2+BG2,
,AB2=AG2+BG2,
∴AG⊥BG.
∵CG![]() BG=G,∴AG⊥平面CBG,
BG=G,∴AG⊥平面CBG,
∵AG![]() 平面AGC,故平面AGC⊥平面BGC.
平面AGC,故平面AGC⊥平面BGC.
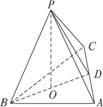
(2)如图所示,由(1)知面AGC⊥平面BGC,且交于GC,在平面BGC内作BH⊥GC,
垂足为H,则BH⊥平面AGC,
∴∠BGH是GB与平面AGC所成的角,
∴Rt△CBG中。
BH=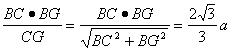
又BG=![]() .∴sin∠BGH=
.∴sin∠BGH=![]() .
.

(3)由(2)知,BH⊥面AGC,作BO⊥AC,垂足为O,则HO⊥AC,
∴∠BOH为二面角B―AC―G的平面角。
在Rt △ABC中,BO=![]()
![]() ,在Rt△BOH中,sin∠BOH=
,在Rt△BOH中,sin∠BOH=![]() ,
,
∠BOH=arcsin![]() ,即二面角B―AG―G的大小为arcsin
,即二面角B―AG―G的大小为arcsin![]()

练习册系列答案
相关题目