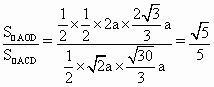题目内容
| |||||||||||
，∠CAB＝
，∠BAD＝
答案：
解析：
解析：
(1) |
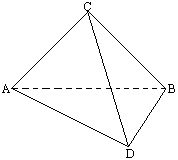
如图所示，∵平面ABC⊥平面ABD，BD⊥AB ∴BD⊥平面ABC 又 AC ∴BD⊥AC 又 BC⊥AC ∴AC⊥平面BCD ∴平面ACD⊥平面BCD |
(2) |
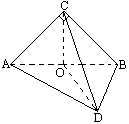
取AB中点O，连结CO、OD，CO⊥平面ABD，设二面角C－AD－B的大小为θ，CO＝a， 则cosθ＝ ∴二面角C－AD－B的大小为arccos |
平面ABC，
练习册系列答案
相关题目
平面ABC，CE//PA，PA=2CE=2。 
平面APB； （2）求二面角A—BE—P的正弦值。
