Question

【题目】已知函数f（x）= ，其中a＞0且a≠1．若a= 时方程f（x）=b有两个不同的实根，则实数b的取值范围是；若f（x）的值域为[2，+∞），则实数a的取值范围是 ．

Answer 1

【答案】["（2， ）","[ ，1）∪（1，+∞）"]
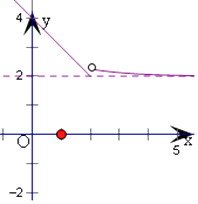
【解析】解：作出f（x）= 的图象，

由a= 时方程f（x）=b有两个不同的实根，

可得b＞2，且b＜2+0.52= ，

即有b∈（2， ）；

函数f（x）= ，

当0＜a＜1时，x≤2时，f（x）=4﹣x≥2，

x＞2时，f（x）=ax+2a+1递减，

可得2a+1＜f（x）＜a2+2a+1，

f（x）的值域为[2，+∞），可得2a+1≥2，解得 ≤a＜1；

当a＞1时，x≤2时，f（x）=4﹣x≥2，

x＞2时，f（x）=ax+2a+1递增，

可得f（x）＞a2+2a+1＞4，

则f（x）的值域为[2，+∞）成立，a＞1恒成立．

综上可得a∈[ ，1）∪（1，+∞）．

所以答案是：（2， ），[ ，1）∪（1，+∞）．