题目内容
已知命题p:“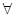 x∈[1,2],2x2-a≥0”,命题q:“
x∈[1,2],2x2-a≥0”,命题q:“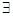 x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
x∈R,x2+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围。
【答案】
a≤-2或1≤ a≤2.
【解析】
试题分析:p:y=2x2在x∈[1,2]递增,最小值为2,所以a≤2. 4分
q:Δ=4a2-4(2-a)≥0,∴a2+a-2≥0,a≤-2或a≥1 . 8分
若命题“p且q”是真命题,则p、q都为真. 12分
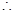 a≤-2或1≤ a≤2.
14分
a≤-2或1≤ a≤2.
14分
考点:本题考查了充要条件的判断
点评:利用等价命题先进行命题的等价转化,搞清楚命题中条件与结论的关系,再去解不等式,找解集间的包含关系,进而使问题解决

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知命题p:?x∈R,2x2+2x+
<0;命题q:?x∈R,sinx-cosx=
.则下列判断正确的是( )
| 1 |
| 2 |
| 2 |
| A、p是真命题 |
| B、q是假命题 |
| C、¬P是假命题 |
| D、¬q是假命题 |